مقدمه:
انرژی نقطه صفر یا انرژی نوسان خلاء، اصطلاحاتی است که برای نوسانات تصادفی امواج الکترومغناطیسی در خلاء بکار برده می شود. این انرژی پس از حذف تمام انرژی های موجود در محیط، مشاهده می شود. مفهوم انرژی نقطه صفر نخستین بار توسط اینشتین و اوتو استرن1 در سال 1913 تحت عنوان "انرژی رسوبی"2 یا " انرژی مبهم صفر"3 مطرح شد. همه ی پایانه های کوانتومی دارای یک مقدار انرژی نقطه صفر هستند. این اصطلاح عموماً برای حالت های کوانتومی نوسانات هماهنگی بکار می رود که در آن نوسان کننده ای وجود ندارد. در کیهان شناختی نیز انرژی خلاء مبنای ثابت کیهان شناختی است. نمونه آزمایشی انرژی نقطه صفر مستقیما توسط اثر کاسیمیر 4 در مقیاس نانو مشاهده شد5. یک روش برای توضیح این پدیده، استفاده از اصل عدم قطعیت مکانیک کوانتومی است که به موجب آن، انرژی نمی تواند بطور مطلق صفر باشد. در این نوشته با توجه با جابه جایی بسمت آبی گرانش و اثر مسبوئر و آزمایش پوند- ربکا ، از دیدگاه میدان هیگز، با در نظر گرفتن کنش بین گرانش و فوتون، انرژی نقطه صفر توضیح داده می شود. اثر مسبوئر نشان می دهد که هنگام چابه جایی بسمت آبی گرانش، سه نوع بوزون هیگز مختلف موجب افزایش جرم فوتون می شود. این بوزونهای هیگز بار-رنگ مثبت، بار-رنگ منفی و مغناطیس-رنگ نامیده می شوند. با توجه به این بوزونهای هیگز رنگی و معادله دیراک می توان انرژی نقطه صفر را توضیح داد.
2 – فوتون و میدان گرانشی نگرشی متفاوت به رفتار فوتون در میدان گرانش، می تواند ما را در توضیح انرژی نقطه صفر رهنمون گردد. میدانهای الکترومغناطیسی اطراف یک پرتو نوری، میدانهای استاتیکی نیستند و در مقایسه با میدان گرانشی، بسیار قوی ترند. هنگامیکه یک فوتون در میدان گرانشی سقوط می کند، انرژی (جرم) آن افزایش می یابد. با توجه به [SUP]
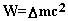 [/SUP]نیروی گرانشی روی فوتون کار انجام می دهد و در نتیجه جرم (انرژی) آن افزایش می یابد. اما انرژی فوتون وابسته به انرژی میدانهای الکتریکی و مغناطیسی آن است. بنابراین هنگام افزایش انرژی فوتون در میدان گرانشی، یک قسمت از کار انجام شده روی فوتون به انرژی الکتریکی و قسمت دیگر آن به انرژی مغناطیسی تبدیل می شود. با استفاده از بوزنهای هیگز که روش جرم دار شدن ذرات را نشان می دهد، چگونه می توانیم این پدیده را توجیه کنیم؟ همچنین با توجه به بوزونهای هیگز، هنگام جابه جایی بسمت آبی گرانش، این فرایند چگونه اتفاق می افتد؟ 3 بار-رنگها و مغناطیس- رنگ بسامد فوتون در میدان گرانشی طبق رابطه زیر تغییر می کند:
[/SUP]نیروی گرانشی روی فوتون کار انجام می دهد و در نتیجه جرم (انرژی) آن افزایش می یابد. اما انرژی فوتون وابسته به انرژی میدانهای الکتریکی و مغناطیسی آن است. بنابراین هنگام افزایش انرژی فوتون در میدان گرانشی، یک قسمت از کار انجام شده روی فوتون به انرژی الکتریکی و قسمت دیگر آن به انرژی مغناطیسی تبدیل می شود. با استفاده از بوزنهای هیگز که روش جرم دار شدن ذرات را نشان می دهد، چگونه می توانیم این پدیده را توجیه کنیم؟ همچنین با توجه به بوزونهای هیگز، هنگام جابه جایی بسمت آبی گرانش، این فرایند چگونه اتفاق می افتد؟ 3 بار-رنگها و مغناطیس- رنگ بسامد فوتون در میدان گرانشی طبق رابطه زیر تغییر می کند:
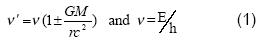
انرژی نقطه صفر یا انرژی نوسان خلاء، اصطلاحاتی است که برای نوسانات تصادفی امواج الکترومغناطیسی در خلاء بکار برده می شود. این انرژی پس از حذف تمام انرژی های موجود در محیط، مشاهده می شود. مفهوم انرژی نقطه صفر نخستین بار توسط اینشتین و اوتو استرن1 در سال 1913 تحت عنوان "انرژی رسوبی"2 یا " انرژی مبهم صفر"3 مطرح شد. همه ی پایانه های کوانتومی دارای یک مقدار انرژی نقطه صفر هستند. این اصطلاح عموماً برای حالت های کوانتومی نوسانات هماهنگی بکار می رود که در آن نوسان کننده ای وجود ندارد. در کیهان شناختی نیز انرژی خلاء مبنای ثابت کیهان شناختی است. نمونه آزمایشی انرژی نقطه صفر مستقیما توسط اثر کاسیمیر 4 در مقیاس نانو مشاهده شد5. یک روش برای توضیح این پدیده، استفاده از اصل عدم قطعیت مکانیک کوانتومی است که به موجب آن، انرژی نمی تواند بطور مطلق صفر باشد. در این نوشته با توجه با جابه جایی بسمت آبی گرانش و اثر مسبوئر و آزمایش پوند- ربکا ، از دیدگاه میدان هیگز، با در نظر گرفتن کنش بین گرانش و فوتون، انرژی نقطه صفر توضیح داده می شود. اثر مسبوئر نشان می دهد که هنگام چابه جایی بسمت آبی گرانش، سه نوع بوزون هیگز مختلف موجب افزایش جرم فوتون می شود. این بوزونهای هیگز بار-رنگ مثبت، بار-رنگ منفی و مغناطیس-رنگ نامیده می شوند. با توجه به این بوزونهای هیگز رنگی و معادله دیراک می توان انرژی نقطه صفر را توضیح داد.
2 – فوتون و میدان گرانشی نگرشی متفاوت به رفتار فوتون در میدان گرانش، می تواند ما را در توضیح انرژی نقطه صفر رهنمون گردد. میدانهای الکترومغناطیسی اطراف یک پرتو نوری، میدانهای استاتیکی نیستند و در مقایسه با میدان گرانشی، بسیار قوی ترند. هنگامیکه یک فوتون در میدان گرانشی سقوط می کند، انرژی (جرم) آن افزایش می یابد. با توجه به [SUP]
