[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]مكانیك كلاسیك یكی از قدیمیترین و آشناترین شاخههای فیزیك است. این شاخه با اجسام در حال سكون و حركت ، و شرایط سكون و حركت آنها تحت تاثیر نیروهای داخلی و خارجی ، سرو كار دارد. قوانین مكانیك به تمام گستره اجسام ، اعم از میكروسكوپی یا ماكروسكوپی، از قبیل الكترونها در اتمها و سیارات در فضا یا حتی به كهكشانها در بخشهای دور دست جهان اعمال میشود. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]مكانیك كلاسیك یكی از قدیمیترین و آشناترین شاخههای فیزیك است. این شاخه با اجسام در حال سكون و حركت ، و شرایط سكون و حركت آنها تحت تاثیر نیروهای داخلی و خارجی ، سرو كار دارد. قوانین مكانیك به تمام گستره اجسام ، اعم از میكروسكوپی یا ماكروسكوپی، از قبیل الكترونها در اتمها و سیارات در فضا یا حتی به كهكشانها در بخشهای دور دست جهان اعمال میشود.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]سینماتیك حركت:
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]سینماتیك به توصیف هندسی محض حركت ( یا مسیرهای) اجسام ، بدون توجه به نیروهایی كه این حركت را ایجاد كردهاند ، میپردازد. در این بررسی عاملین حركت (نیروهای وارد بر جسم) مد نظر نیست و با مفاهیم مكان ، سرعت ، شتاب ، زمان و روابط بین آنها سروكار دارد. در این علم ابتدا اجسام را بصورت ذره نقطهای بررسی نموده و سپس با مطالعه حركت جسم صلب حركت واقعی اجسام دنبال میشود.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]حركت اجسام به دو صورت مورد بررسی است: [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]دینامیك حركت : [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]دینامیك به نیروهایی كه موجب تغییر حركت یا خواص دیگر ، از قبیل شكل و اندازه اجسام میشوند میپردازد. این بخش ما را با مفاهیم نیرو و جرم و قوانین حاكم بر حركت اجسام هدایت میكند. یك مورد خاص در دینامیك ایستاشناسی است كه با اجسامی كه تحت تاثیر نیروهای خارجی در حال سكون هستند سروكار دارد.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]پایه گذاران مكانیك كلاسیك: [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]موارد شكست فرمولبندی اسحاق نیوتن : [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]شكست مكانیك كلاسیك در این وضعیتها ، نتیجه نارسایی مفاهیم كلاسیكی فضا و زمان است.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]مكمل مكانیك كلاسیك: [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]مشكلات موجود در سر راه مكانیك كلاسیك منجر به پیدایش دو نظریه زیر شد:
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]اطلاعات اولیه [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]كاربرد مستقیم قوانین حركت نیوتن برای حركت سیستمهای ساده راحت و آسان است. اما در صورتی كه تعداد ذرات سیستم بیشتر شود، در این صورت استفاده از قوانین نیوتن كار دشواری خواهد بود. در این حالت از یك روش عمومی ، پیچیده و بسیار دقیق كه به همت ریاضیدان فرانسوی ژوزف لویی لاگرانژ ابداع شده است، استفاده میشود. به این ترتیب میتوان معادلات حركت برای تمام سیستمهای دینامیكی را پیدا كرد. این روش چون نسبت به معادلات نیوتن حالت كلی تری دارد، لذا در مورد حالتهای ساده كه با معادلات حركت نیوتن به راحتی حل میشود، نیز قابل اعمال است. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]مختصات تعمیم یافته [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]موقعیت یك ذره در فضا را میتوان با سه سیستم مختصات مشخص كرد. این سیستمها عبارتند از سیستمهای كارتزین ، كروی و استوانهای ، یا در حقیقت هر سه پارامتر مناسب دیگری كه انتخاب شده باشند. اگر ذره مجبور به حركت در یك صفحه یا سطح ثابت باشد فقط به دو مختصه برای مشخص كردن موقغیت ذره نیاز است، در حالیكه اگر ذره روی یك خط مستقیم یا یك منحنی ثابت حركت كند، ذكر یك مختصه كافی خواهد بود. اما در مورد یك سیستم متشكل از N ذره ، برای تشخیص كامل موقعیت همزمان تمام ذرات به 3N مختصه نیاز خواهیم داشت.
اگر محدودیتهای بر سیستم اعمال شده باشد، تعداد مختصات لازم برای مشخص كردن پیكربندی كمتر از 3N خواهد بود. به عنوان مثال ، اگر سیستم مورد نظر یك جسم صلب باشد، برای مشخص كردن پیكربندی آن فقط به موقعیت مكانی یك نقطه مرجع مناسب از جسم (مثلا مركز جرم) و جهت یابی آن نقطه در فضا احتیاج داریم. بنابراین در حالت كلی برای مشخص كردن پیكربندی یك سیستم خاص ، احتیاج به تعداد حداقل معین n مختصه نیاز است. این مختصات را مختصات تعمیم یافته میگویند. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]نیروی تعمیم یافته [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]در سیستم مختصات تعمیم یافته ، به جای نیروهایی كه در مكانیك كلاسیك نیوتنی معمول است، مرتبط با هر مختصه نیرویی تعریف میشود كه به نام نیروی تعمیم یافته معروف است. این كمیت كه با استفاده از تعریف كار محاسبه میشود، به این صورت است كه حاصل ضرب آن در مختصه تعمیم یافته دارای ابعاد كار است. بنابراین اگر مختصه تعمیم یافته دارای بعد فاصله باشد در این صورت این كمیت از جنس نیرو خواهد بود. در صورتیكه مختصه تعمیم یافته از نوع زاویه باشد، در این صورت این كمیت دارای بعد گشتاور خواهد بود. یعنی متناسب با نوع مختصه تصمیم یافته میتواند از جنس نیرو و یا گشتاور نیرو باشد. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]معادلات لاگرانژ [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]برای بررسی حركت یك سیستم در مكانیك لاگرانژی انرژی جبنشی و انرژی پتانسیل سیستم را تعیین میكنند. این كار به این صورت میگیرد كه در مكانیك لاگرانژین در مورد هر سیستم دو كمیت جدید به نامهای لاگرانژین و هامیلتونین تعریف میشود. لاگرانژین برابر تفاضل انرژی پتانسیل از انرژی جنبشی است. در صورتی كه هامیلتون برابر با مجموع انرژی جنبشی و انرژی پتانسیل سیستم است. در واقع میتوان گفت كه كار اصلی تعیین و محاسبه صحیح انرژی جنبشی و پتانسیل است.
سپس این مقادیر در معادلهای كه به معادله لاگرانژ حركت معروف است قرار داده میشود. معادله لاگرانژ ، معادلهای است كه بر حسب مشتقات تابع لاگرانژی نسبت به مختصات تعمیم یافته و نیز مشتق زمانی مشتقات تابع لاگرانژی نسبت به سرعتهای تعمیم یافته نوشته شده است. به عبارت دیگر اگر تابع لاگرانژی را با L نشان دهیم و مختصات تعمیم یافته را با qk و سرعتهای تعمیم یافته را با qk (كه نقطه بیانگر مشتق زمانی مختصه تعمیم یافته qk است) نشان دهیم، معادلات لاگرانژ به صورت زیر خواهد بود:
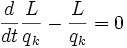
در صورتی كه نیروهای موجود در سیستم همگی پایستار نباشند، به عنوان مثال یك نیروی غیر پایستار مانند اصطكاك وجود داشته باشد در این صورت در طرف دوم معادلات لاگرانژ عبارت Qk كه بیانگر نیروی تعمیم یافته غیر پایستار است، نیز اضافه میشود.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]معادلات لاگرانژ برای تمام مختصات یكسان هستند. این معادلات ، روش یك نواختی برای بدست آوردن معادلات دیفرانسیل حركت یك سیستم در انواع سیستمهای ارائه خواهند داد. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]اصل تغییرات هامیلتون [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]روش دیگر برای استنتاج معادلات لاگرانژ اصل تغییرات هامیلتونی است. در این حالت همانگونه كه قبلا نیز اشاره شد در مورد هر سیستم كمیتی به نام تابع هامیلتونی تعریف میشود كه برابر با مجموع انرژی جنبشی و انرژی پتانسیل سیستم است. این اصل در سال 1834 توسط ریاضیدان اپرلندی ویلیام .ر. هامیلتون ارائه شد.
در این روش فرض میشود كه یك تابع پتانسیل وجود دارد، یعنی سیستم تحت بررسی یك سیستم پایاست. ولی اگر تعدادی از نیروها نیز غیر پایستار باشد مانند مورد معادلات لاگرانژ میتوان سهم این نیرو ها را نیز بطور جداگانه منظور كرد. یعنی در این حالت تابع هامیلتون برابر با مجموع انرژی جنبشی و كار انجام شده توسط تمام نیروها اعم از نیروهای پایستار و غیر پایستار است. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]معادلات هامیلتون [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]معدلات هامیلتون از 2n معادله دیفرانسیل درجه اول تشكیل شده است. این معادلات بر حسب اندازه حركت تعمیم یافته و مشتقات آن نوشته میشود. اندازه حركت تعمیم یافته به صورت مشتقات تابع لاگرانژی نسبیت به سرعت تعمیم یافته تعریف میشود. بنابراین این معادلات زیر خواهند بود.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]در عبارت فوق qk بیانگر سرعت تعمیم یافته است و علامت نقطه در بالای Pk (اندازه حركت تعمیم یافته) بیانگر مشتق زمانی است. اگر معادلات هامیلتون را با معادلات لاگرانژی مقیسه كنیم ملاحظه میشود كه تعداد اولین معادلات زیاد است. یعنی اگر سیستم V با N مختصه یافته مشخص شود، در این صورت معادلات هامیلتون شامل 2n معادله دیفرانسیل درجه اول هستند، در صورتیكه معادلات لاگرانژ از n معادله درجه دوم تشكیل شده است. بنابراین كار كردن با معادلات هامیلتون راحتتر است. معمولا در مكانیك كوانتومی و مكانیك كاری از معادلات هامیلتون استفاده میشود.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]منبع : [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]www.irdanesh.com/
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]سینماتیك حركت:
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]سینماتیك به توصیف هندسی محض حركت ( یا مسیرهای) اجسام ، بدون توجه به نیروهایی كه این حركت را ایجاد كردهاند ، میپردازد. در این بررسی عاملین حركت (نیروهای وارد بر جسم) مد نظر نیست و با مفاهیم مكان ، سرعت ، شتاب ، زمان و روابط بین آنها سروكار دارد. در این علم ابتدا اجسام را بصورت ذره نقطهای بررسی نموده و سپس با مطالعه حركت جسم صلب حركت واقعی اجسام دنبال میشود.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]حركت اجسام به دو صورت مورد بررسی است: [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]سینماتیك انتقالی:
در این نوع حركت پارامترهای سیستم به صورت خطی هستند و مختصات فضایی سیستمها فقط انتقال مییابد. از اینرو حركت انتقالی مجموعه مورد بررسی قرار میگیرد. كمیت مورد بحث در سینماتیك انتقالی شامل جابهجایی ، سرعت خطی ، شتاب خطی ، اندازه حركت خطی و...میباشد.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]سینماتیك دورانی:
در این نوع حركت برخلاف حركت انتقالی پارامتر اصلی حركت تغییر زاویه میباشد. به عبارتی از تغییر جهت حركت ، سرعت و شتاب زاویهای حاصل میشود. و مختصات فضایی سیستم ها فقط دوران مییابند. جابهجایی زاویهای ، سرعت زاویهای ، شتاب زاویهای و اندازه حركت زاویهای از جمله كمیات مورد بحث در این حركت میباشند.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]دینامیك حركت : [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]دینامیك به نیروهایی كه موجب تغییر حركت یا خواص دیگر ، از قبیل شكل و اندازه اجسام میشوند میپردازد. این بخش ما را با مفاهیم نیرو و جرم و قوانین حاكم بر حركت اجسام هدایت میكند. یك مورد خاص در دینامیك ایستاشناسی است كه با اجسامی كه تحت تاثیر نیروهای خارجی در حال سكون هستند سروكار دارد.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]پایه گذاران مكانیك كلاسیك: [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]با این كه شروع مكانیك از كمیت سرچشمه میگیرد ، در زمان ارسطو فرایند فكری مربوط به آن گسترش سریعی پیدا كرد. اما از قرن هفدهم به بعد بود كه مكانیك توسط گالیله ، هویگنس و اسحاق نیوتن بدرستی پایهگذاری شد. آنها نشان دادند كه اجسام طبق قواعدی حركت میكنند ، و این قواعد به شكل قوانین حركت بیان شدند. مكانیك كلاسیك یا نیوتنی عمدتا با مطالعه پیامدهای قوانین حركت سروكار دارد.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]قوانین سه گانه اسحاق نیوتن راه مستقیم و سادهای به موضوع مكانیك كلاسیك میگشاید.این قوانین عبارتند از:
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]قانون اول نیوتن:
هر جسمی به حالت سكون یا حركت یكنواخت خود در روی یك خط مستقیم ادامه میدهد مگر اینكه یك نیروی خارجی خالص به آن داده شود و آن حالت را تغییر دهد.
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]قانون دوم نیوتن:
آهنگ تغییر تكانه خطی یك جسم با برآیند نیروهای وارد بر آن متناسب بوده و در جهت آن قرار دارد.
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]قانون سوم نیوتن:
این قانون كه به قانون عمل و عكسالعمل معروف است ، اینگونه بیان میشود. هر عملی را عكس العملی است ، مساوی با آن و در خلاف جهت آن.
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]قانون اول نیوتن:
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]فرمولبندی لاگرانژی مكانیك كلاسیك:
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]موارد شكست فرمولبندی اسحاق نیوتن : [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]تا آغاز قرن حاضر . قوانین اسحاق نیوتن بر تمام وضعیتهای شناخته شده كاملا قابل اعمال بودند. مشكل هنگامی بروز كرد كه این فرمولبندی به چند وضعیت معین زیر اعمال شدند:
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]اجسام بسیار سریع:
اجسامی كه با سرعت نزدیك به سرعت نور حركت میكنند.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]اجسام با ابعاد میكروسكوپی مانند الكترونها در اتمها.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]شكست مكانیك كلاسیك در این وضعیتها ، نتیجه نارسایی مفاهیم كلاسیكی فضا و زمان است.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]مكمل مكانیك كلاسیك: [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]مشكلات موجود در سر راه مكانیك كلاسیك منجر به پیدایش دو نظریه زیر شد:
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]فرمولبندی نظریه نسبیت خاص برای اجسام متحرك با سرعت زیاد
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
- [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]فرمولبندی مكانیك كوانتومی برای اجسام با ابعاد میكروسكوپی
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]اطلاعات اولیه [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]كاربرد مستقیم قوانین حركت نیوتن برای حركت سیستمهای ساده راحت و آسان است. اما در صورتی كه تعداد ذرات سیستم بیشتر شود، در این صورت استفاده از قوانین نیوتن كار دشواری خواهد بود. در این حالت از یك روش عمومی ، پیچیده و بسیار دقیق كه به همت ریاضیدان فرانسوی ژوزف لویی لاگرانژ ابداع شده است، استفاده میشود. به این ترتیب میتوان معادلات حركت برای تمام سیستمهای دینامیكی را پیدا كرد. این روش چون نسبت به معادلات نیوتن حالت كلی تری دارد، لذا در مورد حالتهای ساده كه با معادلات حركت نیوتن به راحتی حل میشود، نیز قابل اعمال است. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]مختصات تعمیم یافته [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]موقعیت یك ذره در فضا را میتوان با سه سیستم مختصات مشخص كرد. این سیستمها عبارتند از سیستمهای كارتزین ، كروی و استوانهای ، یا در حقیقت هر سه پارامتر مناسب دیگری كه انتخاب شده باشند. اگر ذره مجبور به حركت در یك صفحه یا سطح ثابت باشد فقط به دو مختصه برای مشخص كردن موقغیت ذره نیاز است، در حالیكه اگر ذره روی یك خط مستقیم یا یك منحنی ثابت حركت كند، ذكر یك مختصه كافی خواهد بود. اما در مورد یك سیستم متشكل از N ذره ، برای تشخیص كامل موقعیت همزمان تمام ذرات به 3N مختصه نیاز خواهیم داشت.
اگر محدودیتهای بر سیستم اعمال شده باشد، تعداد مختصات لازم برای مشخص كردن پیكربندی كمتر از 3N خواهد بود. به عنوان مثال ، اگر سیستم مورد نظر یك جسم صلب باشد، برای مشخص كردن پیكربندی آن فقط به موقعیت مكانی یك نقطه مرجع مناسب از جسم (مثلا مركز جرم) و جهت یابی آن نقطه در فضا احتیاج داریم. بنابراین در حالت كلی برای مشخص كردن پیكربندی یك سیستم خاص ، احتیاج به تعداد حداقل معین n مختصه نیاز است. این مختصات را مختصات تعمیم یافته میگویند. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]نیروی تعمیم یافته [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]در سیستم مختصات تعمیم یافته ، به جای نیروهایی كه در مكانیك كلاسیك نیوتنی معمول است، مرتبط با هر مختصه نیرویی تعریف میشود كه به نام نیروی تعمیم یافته معروف است. این كمیت كه با استفاده از تعریف كار محاسبه میشود، به این صورت است كه حاصل ضرب آن در مختصه تعمیم یافته دارای ابعاد كار است. بنابراین اگر مختصه تعمیم یافته دارای بعد فاصله باشد در این صورت این كمیت از جنس نیرو خواهد بود. در صورتیكه مختصه تعمیم یافته از نوع زاویه باشد، در این صورت این كمیت دارای بعد گشتاور خواهد بود. یعنی متناسب با نوع مختصه تصمیم یافته میتواند از جنس نیرو و یا گشتاور نیرو باشد. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]معادلات لاگرانژ [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]برای بررسی حركت یك سیستم در مكانیك لاگرانژی انرژی جبنشی و انرژی پتانسیل سیستم را تعیین میكنند. این كار به این صورت میگیرد كه در مكانیك لاگرانژین در مورد هر سیستم دو كمیت جدید به نامهای لاگرانژین و هامیلتونین تعریف میشود. لاگرانژین برابر تفاضل انرژی پتانسیل از انرژی جنبشی است. در صورتی كه هامیلتون برابر با مجموع انرژی جنبشی و انرژی پتانسیل سیستم است. در واقع میتوان گفت كه كار اصلی تعیین و محاسبه صحیح انرژی جنبشی و پتانسیل است.
سپس این مقادیر در معادلهای كه به معادله لاگرانژ حركت معروف است قرار داده میشود. معادله لاگرانژ ، معادلهای است كه بر حسب مشتقات تابع لاگرانژی نسبت به مختصات تعمیم یافته و نیز مشتق زمانی مشتقات تابع لاگرانژی نسبت به سرعتهای تعمیم یافته نوشته شده است. به عبارت دیگر اگر تابع لاگرانژی را با L نشان دهیم و مختصات تعمیم یافته را با qk و سرعتهای تعمیم یافته را با qk (كه نقطه بیانگر مشتق زمانی مختصه تعمیم یافته qk است) نشان دهیم، معادلات لاگرانژ به صورت زیر خواهد بود:
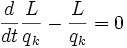
در صورتی كه نیروهای موجود در سیستم همگی پایستار نباشند، به عنوان مثال یك نیروی غیر پایستار مانند اصطكاك وجود داشته باشد در این صورت در طرف دوم معادلات لاگرانژ عبارت Qk كه بیانگر نیروی تعمیم یافته غیر پایستار است، نیز اضافه میشود.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
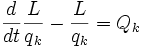
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]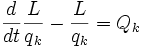
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]معادلات لاگرانژ برای تمام مختصات یكسان هستند. این معادلات ، روش یك نواختی برای بدست آوردن معادلات دیفرانسیل حركت یك سیستم در انواع سیستمهای ارائه خواهند داد. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]اصل تغییرات هامیلتون [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]روش دیگر برای استنتاج معادلات لاگرانژ اصل تغییرات هامیلتونی است. در این حالت همانگونه كه قبلا نیز اشاره شد در مورد هر سیستم كمیتی به نام تابع هامیلتونی تعریف میشود كه برابر با مجموع انرژی جنبشی و انرژی پتانسیل سیستم است. این اصل در سال 1834 توسط ریاضیدان اپرلندی ویلیام .ر. هامیلتون ارائه شد.
در این روش فرض میشود كه یك تابع پتانسیل وجود دارد، یعنی سیستم تحت بررسی یك سیستم پایاست. ولی اگر تعدادی از نیروها نیز غیر پایستار باشد مانند مورد معادلات لاگرانژ میتوان سهم این نیرو ها را نیز بطور جداگانه منظور كرد. یعنی در این حالت تابع هامیلتون برابر با مجموع انرژی جنبشی و كار انجام شده توسط تمام نیروها اعم از نیروهای پایستار و غیر پایستار است. [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]معادلات هامیلتون [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]معدلات هامیلتون از 2n معادله دیفرانسیل درجه اول تشكیل شده است. این معادلات بر حسب اندازه حركت تعمیم یافته و مشتقات آن نوشته میشود. اندازه حركت تعمیم یافته به صورت مشتقات تابع لاگرانژی نسبیت به سرعت تعمیم یافته تعریف میشود. بنابراین این معادلات زیر خواهند بود.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
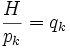
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]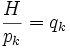
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]
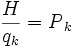
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]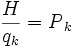
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]در عبارت فوق qk بیانگر سرعت تعمیم یافته است و علامت نقطه در بالای Pk (اندازه حركت تعمیم یافته) بیانگر مشتق زمانی است. اگر معادلات هامیلتون را با معادلات لاگرانژی مقیسه كنیم ملاحظه میشود كه تعداد اولین معادلات زیاد است. یعنی اگر سیستم V با N مختصه یافته مشخص شود، در این صورت معادلات هامیلتون شامل 2n معادله دیفرانسیل درجه اول هستند، در صورتیكه معادلات لاگرانژ از n معادله درجه دوم تشكیل شده است. بنابراین كار كردن با معادلات هامیلتون راحتتر است. معمولا در مكانیك كوانتومی و مكانیك كاری از معادلات هامیلتون استفاده میشود.
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif] [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]منبع : [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]www.irdanesh.com/
