-
توجه: در صورتی که از کاربران قدیمی ایران انجمن هستید و امکان ورود به سایت را ندارید، میتوانید با آیدی altin_admin@ در تلگرام تماس حاصل نمایید.
اگه گراف بلدین لطفا کمک کنید!!
- شروع کننده موضوع zohrejOon
- تاریخ شروع
سلام/من اینو پیدا کردم واسه شما بخونید شاید به دردتون بخوره ..من خودم شخصا اطلاعی ندارم تو این زمینه...
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
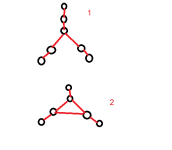
گراف بازه ها:
فرض می کنیم مجموعه ای از بازه های باز داریم. اگر این بازه ها را به عنوان رئوس و اتصال دو راس را، به شرط ناتهی بودن اشتراک بازه های متناظر، یال ها در نظر بگیریم، گرافی می توان رسم کرد که به آن گراف بازی ها میگوییم. به عبارت دریگر گراف بازه ای متناظر با بازی های باز
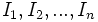گرافی است که رئوس آن بازه های باز
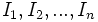بوده و در صورتی دو راس مجاورند(میانشان یال وجود دارد) که بازه های متناظر آن دو راس اشتراک ناتهی داشته باشند.
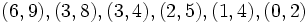
پاسخ: دو بازه
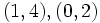اشتراک ناتهی دارند، لذا راس های متناظر این دو بازه را با یک یال به هم وصل می کنیم. ولی دو بازه
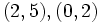اشتراکشان تهی است، پس راس هایی متناظر این دو بازه به هم وصل نمی شوند. به این ترتیب به همین استدلال نمودار گراف بازه ای شش بازه فوق به صورت زیر در می آید:
نحوه تشخیص گراف بازه ای:
سوالی که پیش می آید این است که چگونه می توان تشخیص داد که یک گراف بازه ای است یا نه؟
به عنوان مثال می خواهیم تحقیق کنیم که آیا این گراف بازه ای است یا نه:
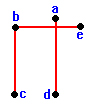
سعی می کنیم بازه هایی را بیابیم که گراف متناظر آنها (گراف بازه ای آنها) به این صورت باشد.
5 بازه زیر را در نظر می گیریم:
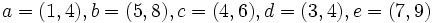
(دقت شود که دو بازه a و b نباید اشتراک داشته باشند)
مشاهده می شود گراف متناظر با این بازه ها به صورت گراف داده شده است پس این گراف بازه ای است.
حال به این نمونه توجه کنید. می خواهیم بازه ای بودن این گراف را بررسی کنیم:
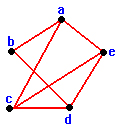
قبل از بررسی کردن به توضیحات زیر توجه کنید:
فرض می کنیم دور مرتبه 4 مقابل خود یک گراف یا قسمتی از یک گراف باشد:
نشان می دهیم این گراف و یا گرافی شامل این دور بازه ای نمی باشد. به برهان خلف اگر این گراف یا گراف شامل ایت دور بازه ای باشد:
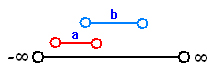
روی محور اعداد حقیقی برای هر یک از راس ها بازه ای به صورت زیر در نظر می گیریم:
چون a با b مجاور است باید روی محور اعداد بازه های متناظر با این دو راس دارای اشتراک باشند مطابق شکل:
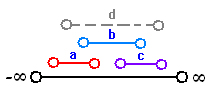
از طرفی c نیز با b مجاور است و با a مجاور نمی باشد پس بازه متناظر با c با بازه b اشتراک دارد ولی با بازه متناظر a اشتراک ندارد. مطابق شکل:
حال چون d هم با a و هم با c مجاور است پس بازه متناظر با راس d باید به گونه ای اشد که هم به a و هم به c اشتراک داشته باشد و این تناقض است چرا که در این صورت d با b هم اشتراک پیدا می کند در حالی که از b به d یالی رسم نشده است.
پس فرض خلف باطل و حکم برقرار است.
پس در این گراف چون abcd یک دور با طول 4 است بنابر دلایل ذکر شده بازه ای نمی باشد.
روش دیگری که می توان بوسیله آن تعیین نمود که گراف بازه ای نمی باشد این است که اگر در گرافی حفره وجود داشت آن گراف بازه ای نمی باشد. مشاهده می شود این روش تعمیمی بر روش استدلال گفته شده در بالا است.
البته این شرط، یک شرط کافی برای غیر بازه ای بودن گراف است و اگر در گرافی حفره مشاهده نشد نمی توان نتیجه گرفت لزوما گراف بازه ای است.
به عنوان مثال گراف زیر دارای حفره نمی باشد ولی در عین حال بازه ای نیز نمی باشد:
abcd یک حفره محسوب می شود و لذا گراف همان طور که گفته شد بازه ای نمی باشد.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
گراف بازه ها:
فرض می کنیم مجموعه ای از بازه های باز داریم. اگر این بازه ها را به عنوان رئوس و اتصال دو راس را، به شرط ناتهی بودن اشتراک بازه های متناظر، یال ها در نظر بگیریم، گرافی می توان رسم کرد که به آن گراف بازی ها میگوییم. به عبارت دریگر گراف بازه ای متناظر با بازی های باز
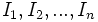
- تذکر: از حساب دیفرانسیل و انتگرال به یاد داریم که بازه ی باز
مجموعه همه اعداد حقیقی بین دو عدد a و b(که شامل خود a و b نمی شود) است.
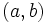
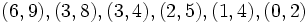
پاسخ: دو بازه
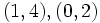
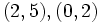
نحوه تشخیص گراف بازه ای:
سوالی که پیش می آید این است که چگونه می توان تشخیص داد که یک گراف بازه ای است یا نه؟
به عنوان مثال می خواهیم تحقیق کنیم که آیا این گراف بازه ای است یا نه:
سعی می کنیم بازه هایی را بیابیم که گراف متناظر آنها (گراف بازه ای آنها) به این صورت باشد.
5 بازه زیر را در نظر می گیریم:
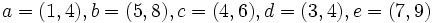
(دقت شود که دو بازه a و b نباید اشتراک داشته باشند)
مشاهده می شود گراف متناظر با این بازه ها به صورت گراف داده شده است پس این گراف بازه ای است.
حال به این نمونه توجه کنید. می خواهیم بازه ای بودن این گراف را بررسی کنیم:
قبل از بررسی کردن به توضیحات زیر توجه کنید:
- در حالت کلی می توان گفت هر گراف دلخواه دارای یک دور از مرتبه 4 گراف بازه ای نمی باشد.
فرض می کنیم دور مرتبه 4 مقابل خود یک گراف یا قسمتی از یک گراف باشد:
نشان می دهیم این گراف و یا گرافی شامل این دور بازه ای نمی باشد. به برهان خلف اگر این گراف یا گراف شامل ایت دور بازه ای باشد:
روی محور اعداد حقیقی برای هر یک از راس ها بازه ای به صورت زیر در نظر می گیریم:
چون a با b مجاور است باید روی محور اعداد بازه های متناظر با این دو راس دارای اشتراک باشند مطابق شکل:
از طرفی c نیز با b مجاور است و با a مجاور نمی باشد پس بازه متناظر با c با بازه b اشتراک دارد ولی با بازه متناظر a اشتراک ندارد. مطابق شکل:
حال چون d هم با a و هم با c مجاور است پس بازه متناظر با راس d باید به گونه ای اشد که هم به a و هم به c اشتراک داشته باشد و این تناقض است چرا که در این صورت d با b هم اشتراک پیدا می کند در حالی که از b به d یالی رسم نشده است.
پس فرض خلف باطل و حکم برقرار است.
پس در این گراف چون abcd یک دور با طول 4 است بنابر دلایل ذکر شده بازه ای نمی باشد.
روش دیگری که می توان بوسیله آن تعیین نمود که گراف بازه ای نمی باشد این است که اگر در گرافی حفره وجود داشت آن گراف بازه ای نمی باشد. مشاهده می شود این روش تعمیمی بر روش استدلال گفته شده در بالا است.
البته این شرط، یک شرط کافی برای غیر بازه ای بودن گراف است و اگر در گرافی حفره مشاهده نشد نمی توان نتیجه گرفت لزوما گراف بازه ای است.
به عنوان مثال گراف زیر دارای حفره نمی باشد ولی در عین حال بازه ای نیز نمی باشد:
- یادآوری(تعریف حفره): در گراف ها هر چهار ضلعی یا n ضلعی (n>3) که بدون قطر باشد را یک حفره می گوییم.
abcd یک حفره محسوب می شود و لذا گراف همان طور که گفته شد بازه ای نمی باشد.
به عنوان مثال گراف زیر دارای حفره نمی باشد ولی در عین حال بازه ای نیز نمی باشد:
چرا خوب؟؟؟