حركت زاويه اي و مداري الكترون

[parisa]

حركت زاويه اي و مداري الكترون
​

همانطور كه مي‌دانيم انرژي موج الكترومغناطيس از رابطه معروف پلانك يعني E=hv بدست مي‌آيد . يعني انرژي موج برابر است با فركانس موج ضربدر ثابت پلانك كه كمترين مقدار ( كوانتاي ) انرژي است و مربوط به يك سيكل يا تواتر موج است . به مطالب زير دقت كنيد :

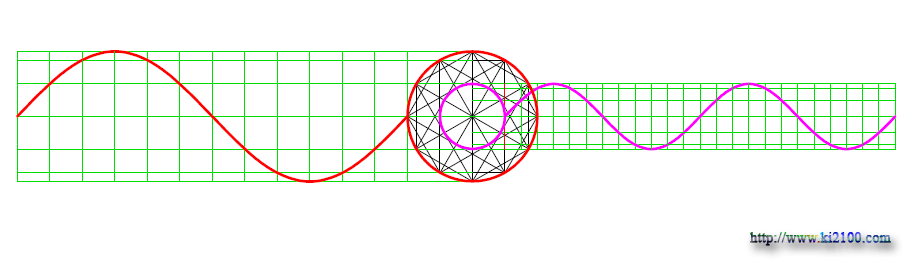
خويشاوندي دايره و موج سينوسي​

​

توضيحات :
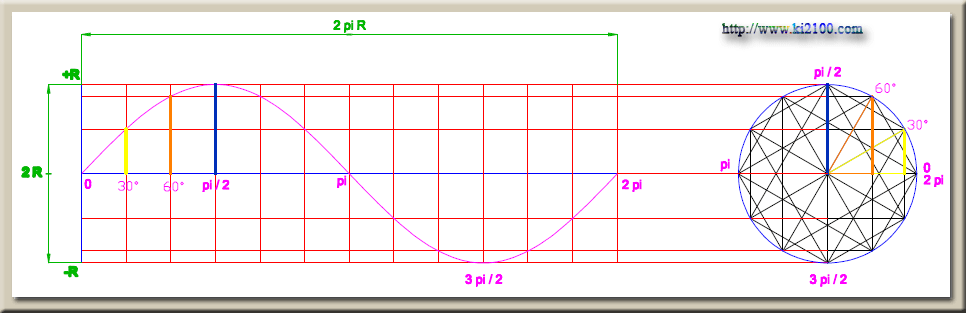
در سمت راست تصوير فوق ، دايره مثلثاتي را به 12 قسمت مساوي و هر كدام 30 درجه يا π/6 تقسيم كرده‌ايم . در سمت چپ تصوير فوق ، دستگاه مختصاتي رسم شده است كه محور افقي آن به طول 2πr يعني محيط دايره و محور عمودي آن ، محور سينوسها ميباشد . طول افقي به 12 قسمت مساوي تقسيم شده كه هر قسمت نشانگر طول كمان 30 درجه است . محور عمودي با خطوط قرمز از مبدا سينوسهاي 30 و 30- ، 60 و 60- ، 90 و 90- مدرج شده و منحني موج سينوسي نقطه‌يابي و رسم شده است . اين رابطه مابين دايره و موج سينوسي به دفعات در فيزيك مشاهده شده است و در رياضيات نيز توجيه پذير است به طور مثال با دوران ( سرعت زاويه‌اي ثابت ) رتور در ميدان مغناطيسي داخل يك دينام ، جرياني با ولتاژ متناوب و به صورت سينوسي پديدار و توليد ميشود . همانطور كه ميدانيم در مكانيك كوانتومي انرژي فوتون نيز از رابطه معروف پلانك بدست مي‌آيد :

E=hν​

​

در واقع انرژي هر تواتر ( سيكل ) موج الكترومغناطيس برابر h ميباشد . به طور خلاصه انرژي يك سيكل طيف قرمز برابر انرژي يك سيكل طيف بنفش است و اين مقدار مستقل از انرژي كلي موج در واحد زمان تعريف شده است و مقدار آن به ثابت پلانك معروف است . اينك اگر اين انرژي ( يك كوانتوم انرژي ) را بر محيط يك دايره به شعاع واحد يك ( مدار فرضي الكترون ) تقسيم كنيم خواهيم داشت :

ћ=h/2π​

​

كه اين مقدار جديد ћ در مكانيك كوانتومي كاربرد دارد و معني آن توزيع انرژي يك سيكل موج بر روي مدار الكترون پيرامون هسته است زيرا الكترون برانگيخته با يك دور كامل چرخش به دور هسته يك سيكل موج الكترومغناطيس توليد و منتشر مي‌كند .

اينك ما سرعت خطي الكترون برانگيخته مربوط به مدار طيف بنفش مريي با فركانس 14^10*8 و همچنين شعاع مدار استاندارد آن را محاسبه مي‌كنيم :

طبق تعريف موج الكترومغناطيس زماني توليد و منتشر ميشود كه الكترون مدار برانگيخته نوسان كند يعني مابين دو تراز تغيير مكان دهد . پس فعلا ميتوان چنين فرض كنيم كه انرژي كل موج مربوط به انرژي جنبشي الكترون روي مدار است يعني :

​

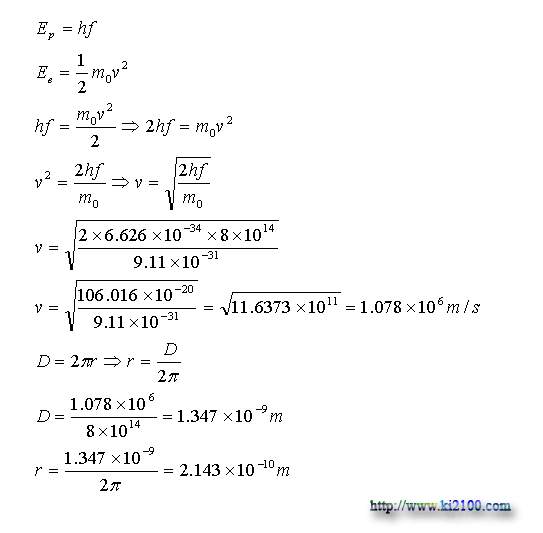
كه در اين محاسبات Ep انرژي فوتون يا موج الكترومغناطيس ، h ثابت پلانك ، f فركانس موج ، Ee انرژي جنبشي الكترون ، m0 جرم سكون الكترون ، v سرعت خطي الكترون روي مدار ، D محيط مدار استاندارد الكترون و r شعاع آن مدار ميباشد . ولي لازم است به دو نكته اشاره كرد :
1- با افزايش عدد اتمي ( تعداد پروتونهاي هسته ) بر تعداد الكترونهاي پيرامون هسته افزوده شده و اين الكترونها نسبت به هم نيرو وارد كرده و تغييراتي در شعاع مدارها بوجود مي‌آيد .
2- با يونيزه شدن اتم اگر اتم الكترون از دست بدهد شعاع مدارها كم شده ولي اگر اتم ، الكترون دريافت كند شعاع مدارها افزايش مي‌يابد .
پس در اتمها شعاع مدارها زياد اهميت ندارد بلكه آنچه مهم است سرعت زاويه‌اي چرخش الكترونها به دور هسته است كه نوسان آنها ميتواند امواج الكترومغناطيسي توليد و منتشر كند .


حركت مداري الكترون :

حركت مداري الكترون را ميتوانيم همان سرعت زاويه‌اي الكترون به دور هسته تعريف كنيم كه درست معادل فركانس ( تواتر يا بسامد ) موج الكترومغناطيس نشري از مدار يا تراز ( لايه و يا زير لايه اتم ) است . به طور مثال حركت مداري الكترون يا سرعت زاويه‌اي آن مربوط به تراز طيف بنفش مريي با فركانس 14^10*8 درست معادل 14^10*8 راديان بر ثانيه است . و اين چرخش مداري در ديد ما هم ميتواند ساعت گرد باشد و هم پا ساعت گرد و ميتواند به سطح و يا حجم يك كره گسترش يابد و شكل هندسي كروي به اتم منفرد بدهد .

اينك سرعت خطي الكترون روي مدار يا تراز انرژي طيف ماوراي بنفش غير مريي با فركانس 17^10 هرتز را محاسبه مي‌كنيم :

​

اينك اين سوال مطرح ميشود كه آيا ممكن است سرعت الكترون در مدار ماكزيمم يعني به اندازه سرعت نور شود ؟
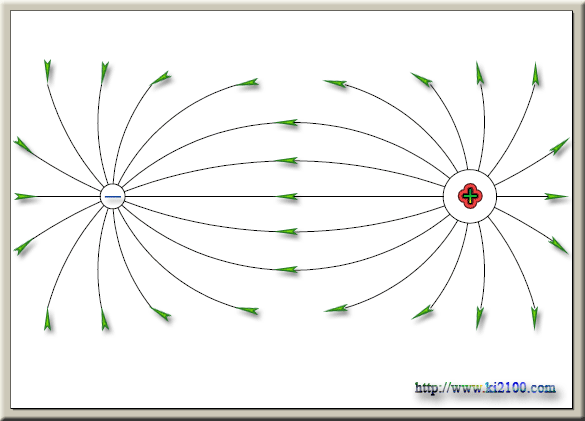
چنين حالتي را ميتوان در زماني تصور كرد كه مثلا الكترون مدار هيدروژن به روي هسته پروتون سقوط كرده و در روي مداري فوق‌العاده نزديك به پروتون بچرخد و ذره سوم ديگري به نام نوترون را بوجود آورند . در اين سقوط الكترون به طرف هسته پروتون ، انرژي زيادي به صورت امواج و تابشهاي الكترومغناطيس منتشر ميشود . نوترون از لحاظ بار الكتريكي همانند اتم هيدروژن خنثي به نظر ميرسد و اين ممكن نخواهد بود مگر اينكه الكترون حول پروتون چرخش داشته باشد كه اگر اينگونه نباشد نتيجه ادغام اين دو ذره ميبايست ذره‌اي با دو قطب الكتريكي غير هم نام همانند شكل زير تشكيل شود كه چنين نيست .

​

اينك حركت مداري يا سرعت زاويه‌اي الكترون فرضي با سرعت نزديك به سرعت نور و همچنين شعاع اين مدار فرضي را محاسبه مي‌كنيم .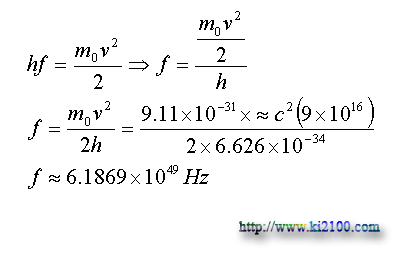

​

كه اين فركانس در محدوده بسامد امواج الكترومغناطيس طولي يا همان امواج گرانشي است .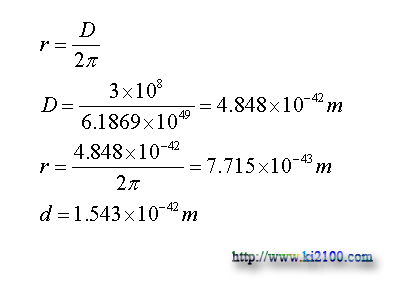

​

كه ميتوان قطر اين نوترون فرضي را نيز بدست آورد كه براي اولين بار به صورت تئوري محاسبه ميشود . اما نكته مهم اينكه در زمان تصادم نوترونها با يكديگر حتي با ذرات و موانع ديگر اين الكترون در مدار فرضي به نوسان در آمده و امواج گرانشي منتشر ميشود كه توان آنها خيلي كم بوده و فعلا قابل شناسايي نيستند ولي اگر اجرام نوتروني سنگين مثل ستارگان نوتروني و يا سياه چاله ها با هم تصادم داشته باشند يا اجرام سنگين مثل سيارات و ستارگان در كام آنها فرو رود امواج گرانشي پرتواني توسط آنها توليد و منتشر خواهد شد كه گذر آنها از منظومه شمسي ميتواند باعث تغيير فاصله مابين زمين و ماه شده و حتي تغييراتي در حجم كروي ماه و زمين ايجاد كند . مبحث محاسبه متريك گرانشي سياه چاله ( جرم نوتروني )


اندازه حركت زاويه‌اي مداري الكترون :

اصل موضوع بوهر

• الكترونها مقيد هستند در مدارهايي حركت كنند كه در آنها اندازه حركت زاويه‌اي الكترونها مضرب درستي از ħ=frach2π باشد . به عبارت ديگر ، در مورد مدارهاي دايره‌اي شكل با شعاع r ، سرعت الكترون (v) بايد از رابطه mvr=nħ تبعيت كند . لازم به ذكر است كه الكترونها در اين مدارها با وجود سرعتي كه دارند ، تابش نمی‌كنند . بنابراين مسيرهاي حركت الكترونها را در اين مدل ، مدارهاي ايستا می‌گويند .
  
  
• الكترونها می‌توانند گذرهاي گسسته‌اي از يك مدار مجاز به مدار مجاز ديگر انجام دهند . تغيير انرژي اين دو تراز به صورت تابشي كه فركانس آن وابسته به تفاضل انرژي اين دو تراز است ، ظاهر می‌شود . اگر اتم ، تابش جذب كند ، باز الكترونها بر اثر اين تابش به يك تراز انرژي بالاتر می‌روند .

مشكل اول اين نظريه رابطه mvr=nħ است . براي اينكه mvr مولفه اندازه حركت ( تكانه ) زاويه‌اي و واحد آن Kg m^2/s ولي nħ مولفه انرژي و واحد آن J/s است كه شايد اين دو مولفه با هم متناسب باشند ولي با اين شرايط هم ارز نخواهند بود ، زيرا همواره رابطه E=Pv/2 مابين انرژي جنبشي ذره ، تكانه و سرعت ذره بر قرار است كه از رابطه E=1/2mv^2 حاصل ميشود .
و از طرفي اگر سيستم متشكل از زمين و خورشيد را در نظر بگيريم ، نيروي جانب مركز ( گريز از مركز ) دوران زمين به دور خورشيد ، معادل نيروي گرانش وارد بر زمين از طرف خورشيد است . با فرض اينكه اين سيستم منزوي است ( از ساير سيارات صرف نظر مي‌كنيم ) لذا اندازه حركت زاويه‌اي زمين L به دور خورشيد نيز ثابت است . بنابراين با توجه به رابطه L=mvr با كاهش فاصله ، سرعت افزايش مي‌يابد ( L اندازه حركت زاويه‌اي زمين ، m جرم زمين ، r فاصله مركز زمين تا مركز خورشيد و v سرعت حركت يا همان سرعت خطي سياره زمين است ) . در واقع زمين به دور مركز خورشيد نمی‌گردد ، بلكه به دور مركز جرم سيستم ( زمين و خورشيد ) می گردد . با تغيير موقعيت زمين نسبت به خورشيد ، مركز جرم [مشترك] نيز تغيير می كند و چنين به نظر مي‌رسد كه مدار حركت بيضی است و خورشيد نيز در يكي از كانون‌هاي آن قرار دارد . در واقع اندازه حركت زاويه اي در مكانيك سيارات كاربرد دارد و ما نميتوانيم به جاي خورشيد ، هسته اتم و به جاي نيروي گرانش ، نيروي كولوني و به جاي زمين ، الكترون و نيروي جانب مركز آن را در نظر بگيريم براي اينكه سرعت زاويه اي ( اسپين ) هسته خيلي زياد است و خطوط ميدان الكتريكي دوران يافته و الكترونها در اين ميادين دايره‌اي شكل و بسته حركت دارند يعني شكل زير :

​

​

ولي همانطور كه توضيح داد شد با يك دور چرخش كامل الكترون برانگيخته به دور هسته ، يك كوانتاي ثابت پلاك انرژي توليد و منتشر ميشود . پس ميتوان به راحتي نتيجه گرفت كه :

E=hω​

يعني انرژي موج الكترومغناطيس (E) برابر است با ثابت پلانك (h) ضربدر سرعت زاويه‌اي مداري الكترون برانگيخته (ω) . يعني ما در فيزيك هيچ انرژي كمتر از انرژي حاصل از چرخش يك الكترون برانگيخته به دور هسته نداريم كه مفهوم واقعي و كلي فيزيك كوانتومي را ميرساند . اين رابطه نشان مي‌دهد كه انرژي كلي موج يا فوتون به سرعت زاويه‌اي مداري الكترون برانگيخته وابسته است و نه به پارامترهاي ديگر .
با توجه به اينكه واحد ω راديان بر ثانيه يا 2π بر ثانيه است ، ثابت پلانك را ميبايست تقسيم بر 2π كنيم تا به همان مقدار قبلي رابطه برسيم يعني ћ=h/2π پس معادله كلي اين خواهد شد :

E=h/2π*ω​

E=ћω​

​

همانطور كه مشخص است الكترون برانگيخته در روي مدار مربوط به طيف بنفش دو چرخش كامل ولي الكترون برانگيخته روي مدار قرمز يك چرخش كامل در واحد زمان انجام داده است ولي همانطور كه ميدانيم انرژي طيف بنفش دو برابر طيف قرمز است براي اينكه در واحد زمان مشخص ، تراز يا مدار بنفش دو سيكل ولي مدار قرمز يك سيكل توليد و منتشر نموده است ولي هر دو طيف مسافت‌هاي مساوي را در واحد زمان طي كرده‌اند يعني همان سرعت ثابت نور . البته ذكر اين نكته ضروري است كه طول موج امواج الكترومغناطيس بيشتر از قطر اتمها ميباشد و شكل فوق صرفا جهت روشن شدن موضوع ارايه شده است .
همانطور كه در مبحث اصل تبادل انرژي كوانتومي توسط لايه‌ها و زير لايه‌ها در اتم‌ها گفته شد :
تعريف : موج الكترومغناطيس توليد شده توسط يك لايه يا يك زير لايه از يك اتم ( تراز انرژي ) ، فقط قابل جذب توسط همان لايه يا زير لايه از اتم ديگر است . به بيان ديگر موج الكترومغناطيس توليد شده توسط يك لايه يا يك زير لايه از يك اتم ، فقط در همان لايه يا زير لايه از اتم ديگر القا يا شارژ ميشود .

​

محمدرضا طباطبايي