حرکت فنر در حال نوسان
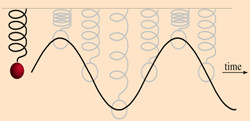
به تغییر تکرارشونده ی یک جسم (در واحد زمان) حول یک وضعیت تعادل، نوسان می گویند. حرکت آونگ یا پاندول ساعت و یا فتر، نمونه‌ای از حرکت نوسانی است. در طی حرکت و نوسان این اجسام، انرژی جنبشی و انرژی پتانسیل آن ها به طور مرتب به هم تبدیل می‌شوند.
به عنوان مثال، در بررسی حرکت آونگ، هنگامی که آونگ در پایین‌ترین نقطه مسیر خود قرار دارد، بیش ترین انرژی جنبشی و کم ترین انرژی پتانسیل را داراست.
به عبارت دیگر، در این لحظه، آونگ بیش ترین سرعت را دارد. در لحظه‌ای که آونگ در حداکثر ارتفاع قرار می‌گیرد، انرژی جنبشی آن صفر است و انرژی پتانسیل آن حداکثر است، یعنی سرعت آونگ در این محل صفر است.
شاید اصطلاحات نوسانگر میرا و غیرمیرا را شنیده باشید؛ در این جا توضیح خواهیم داد که معنای این حرکت ها چیست.
نوسان میرا حالتی است که جسم در حال نوسان بعد از مدتی، حرکت خود را کند کرده و دامنه نوسان آن کاهش پیدا می کند تا جایی که کاملا از حرکت بایستد. اصطکاک، یکی از عوامل کند کننده حرکت یک نوسانگر است.
یکی دیگر از عواملی که ممکن است باعث کند شدن و توقف جسم در حال نوسان شود، از بین رفتن نیروی اولیه ای باشد که آن جسم را وادار به حرکت کرده بود. بنابراین اکثر حرکت های نوسانی اطراف ما میرا هستند؛ چرا که اصطکاک و تمام شدن نیروی وادارنده برای نوسان، غیر قابل اجتناب هستند.
در حالتی که میرایی سیستم صفر باشد، یعنی هیچ گونه اتلاف انرژی و اصطکاکی وجود نداشته باشد، مجموع انرژی پتانسیل و انرژی جنبشی ثابت باقی می‌ماند.
[h=2]نوسانگر هارمونیک ساده: ساده ترین سیستم نوسان، یک جسم متصل به یک فنر خطی است که هیچ نیرویی غیر از جسم متصل به آن در این سیستم وجود نداشته باشد. زمانی سیستم در حالت تعادل است که فنر ساکن باشد. اگر سیستم از حالت تعادل خارج شود، یک نیروی خالص بازگرداننده برای جسم متصل به فنر به وجود می آید.
بسته به این که وضعیت فنر و جرم متصل به آن افقی است یا عمودی و یا در روی سطح شیب دار قرار دارد، معادلات و نیروهای وارد بر سیستم آن ها متفاوت خواهد بود.
بهتر است ابتدا مطالب مربوط به دامنه، فرکانس، انرژی جنبشی و پتانسیل مربوط به سیستم های نوسانی را مطالعه کنید تا مطالب پایین را بهتر متوجه شوید:
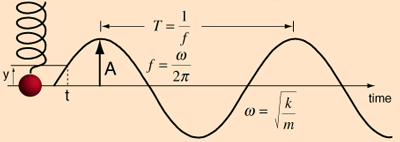
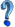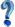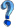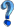
سوال: اگر دوره تناوب فنر در شکل بالا ٢ ثانیه باشد، فرکانس زاویه ای آن چه قدر است؟
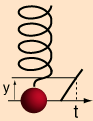
با توجه به رابطه دوره تناوب با فرکانس زاویه ای در شکل بالا، جواب صحیح 14/3 خواهد بود.
معادله حرکت نوسانی ساده به صورت زیر است:
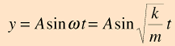در این معادله، A دامنه حرکت، y مکان جسم از وضعیت تعادل است که برای حالت افقی از x به جای y استفاده می شود.
m جرم جسم متصل به فنر، k ثابت فنر و ω فرکانس زاویه ای نوسانگر است.
اگر از معادله بالا یک بار مشتق بگیریم، معادله سرعت نوسان گر به دست می آید؛ با مشتق دوباره از معادله سرعت به معادله شتاب نوسانگر خواهیم رسید.
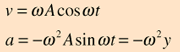
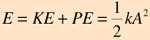بهتر است ابتدا کتاب درسی خود را مطالعه کرده و با مفاهیم اولیه آشنا شوید،. این اثرات با استفاده از یک آهن ربا، پیچه و تغییر دامنه نوسانگر، ذرات ریز (شن) بر روی گره های ناشی از امواج در حال تغییر جمع می شوند. سعی کنید از دبیر خود توضیح بیش تر این بحث را بخواهید.
[h=4]مرکز یادگیری سایت تبیان - تنظیم: آلچالانلو
به عنوان مثال، در بررسی حرکت آونگ، هنگامی که آونگ در پایین‌ترین نقطه مسیر خود قرار دارد، بیش ترین انرژی جنبشی و کم ترین انرژی پتانسیل را داراست.
به عبارت دیگر، در این لحظه، آونگ بیش ترین سرعت را دارد. در لحظه‌ای که آونگ در حداکثر ارتفاع قرار می‌گیرد، انرژی جنبشی آن صفر است و انرژی پتانسیل آن حداکثر است، یعنی سرعت آونگ در این محل صفر است.
شاید اصطلاحات نوسانگر میرا و غیرمیرا را شنیده باشید؛ در این جا توضیح خواهیم داد که معنای این حرکت ها چیست.
نوسان میرا حالتی است که جسم در حال نوسان بعد از مدتی، حرکت خود را کند کرده و دامنه نوسان آن کاهش پیدا می کند تا جایی که کاملا از حرکت بایستد. اصطکاک، یکی از عوامل کند کننده حرکت یک نوسانگر است.
یکی دیگر از عواملی که ممکن است باعث کند شدن و توقف جسم در حال نوسان شود، از بین رفتن نیروی اولیه ای باشد که آن جسم را وادار به حرکت کرده بود. بنابراین اکثر حرکت های نوسانی اطراف ما میرا هستند؛ چرا که اصطکاک و تمام شدن نیروی وادارنده برای نوسان، غیر قابل اجتناب هستند.
شکل موج سینوسی نوسان میرا در زمان |
در حالتی که میرایی سیستم صفر باشد، یعنی هیچ گونه اتلاف انرژی و اصطکاکی وجود نداشته باشد، مجموع انرژی پتانسیل و انرژی جنبشی ثابت باقی می‌ماند.
[h=2]نوسانگر هارمونیک ساده: ساده ترین سیستم نوسان، یک جسم متصل به یک فنر خطی است که هیچ نیرویی غیر از جسم متصل به آن در این سیستم وجود نداشته باشد. زمانی سیستم در حالت تعادل است که فنر ساکن باشد. اگر سیستم از حالت تعادل خارج شود، یک نیروی خالص بازگرداننده برای جسم متصل به فنر به وجود می آید.
بسته به این که وضعیت فنر و جرم متصل به آن افقی است یا عمودی و یا در روی سطح شیب دار قرار دارد، معادلات و نیروهای وارد بر سیستم آن ها متفاوت خواهد بود.
بهتر است ابتدا مطالب مربوط به دامنه، فرکانس، انرژی جنبشی و پتانسیل مربوط به سیستم های نوسانی را مطالعه کنید تا مطالب پایین را بهتر متوجه شوید:
از روی شکل و معادلات مربوط به حرکت نوسانی، به سوال ساده زیر پاسخ دهید:
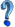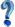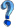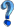
سوال: اگر دوره تناوب فنر در شکل بالا ٢ ثانیه باشد، فرکانس زاویه ای آن چه قدر است؟
با توجه به رابطه دوره تناوب با فرکانس زاویه ای در شکل بالا، جواب صحیح 14/3 خواهد بود.
معادله حرکت نوسانی ساده به صورت زیر است:
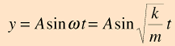
m جرم جسم متصل به فنر، k ثابت فنر و ω فرکانس زاویه ای نوسانگر است.
اگر از معادله بالا یک بار مشتق بگیریم، معادله سرعت نوسان گر به دست می آید؛ با مشتق دوباره از معادله سرعت به معادله شتاب نوسانگر خواهیم رسید.
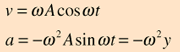
در نوسان گر غیر میرا، که بقای انرژی مکانیکی برقرار است، جمع کل انرژی جنبشی و پتانسیل مقدار ثابتی خواهد بود و در هر قسمت از مسیر نوسان گر، انرژی جنبشی و پتانسیل به هم تبدیل خواهند شد:
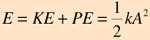
[h=4]مرکز یادگیری سایت تبیان - تنظیم: آلچالانلو