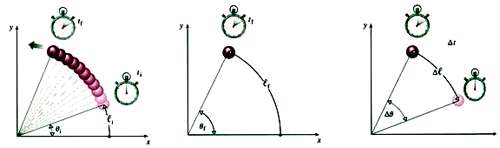
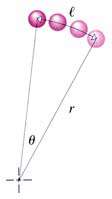
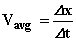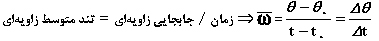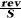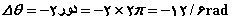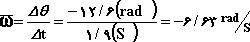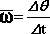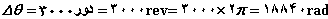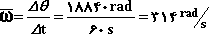سرعت لحظه‌ای زاویه ای حركت دورانی حول یك نقطه ثابت را در نظر بگیرید (مثلاً دوران دانه‌های تسبیح)
همگی ذرّات حول نقطه‌ای در حال دورانند و اگر چه هر كدام در شعاع‌های متفاوت در حركتند ولی همگی یك مقدار زاویه
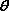را جاروب می‌كنند.
عبارت است از سرعت زاویه‌ای در هر لحظه می‌باشد.برای تعریف آن همان مراحلی را طی می‌كنیم كه برای محاسبه سرعت لحظه‌ای انجام دادیم. برای این منظور زمان
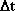را كوچك و كوچكتر در نظر می‌گیریم.
بنابراین متناظراً
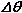نیز كوچك خواهد شد. اگر در یك فرآیند حدی،
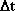به سمت صفر میل كند(
) آنگاه سرعت زاویه‌ای لحظه‌ای برابر خواهد بود با:
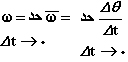
اندازه سرعت لحظه‌ای زاویه‌ای (مستقل از علامت مثبت یا منفی آن) به عنوان سرعت لحظه‌ای زاویه‌ای نامیده می‌شود. بنا به تعریف فوق یك مفهوم مشتق گیری در سرعت زاویه‌ای لحظه‌ای نهفته است. به عبارتی:
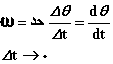
بنابراین با مشتق گیری از رابطه
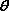نسبت به t می‌توان سرعت زاویه‌ای لحظه‌ای را به دست آورد.
مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا
همگی ذرّات حول نقطه‌ای در حال دورانند و اگر چه هر كدام در شعاع‌های متفاوت در حركتند ولی همگی یك مقدار زاویه
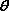
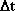
بنابراین متناظراً
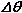
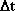
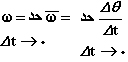
اندازه سرعت لحظه‌ای زاویه‌ای (مستقل از علامت مثبت یا منفی آن) به عنوان سرعت لحظه‌ای زاویه‌ای نامیده می‌شود. بنا به تعریف فوق یك مفهوم مشتق گیری در سرعت زاویه‌ای لحظه‌ای نهفته است. به عبارتی:
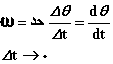
بنابراین با مشتق گیری از رابطه
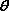
مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا
