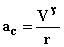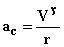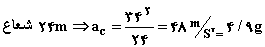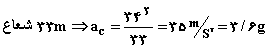شتاب مركزگرا (1)
در این مبحث خواهید دید كه چگونه اندازه شتاب مركزگرا (a[SUB]c[/SUB]) به اندازه تندی و شعاع حركت ارتباط دارد.
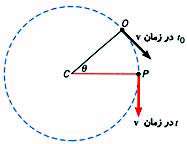
در شكل مقابل یك جسم كه با (٠) نشان داده شده در حال حركت یكنواخت دایروی می‌باشد.
در لحظه t[SUB]٠[/SUB] سرعت آن مماس بر دایره در نقطه o و در لحظه t سرعت آن مماس بر دایره در نقطه p خواهد بود.
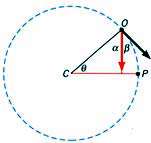
در هنگامی كه جسم از o به p حركت می‌كند، شعاع دایره نیز زاویه
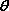را جاروب می‌كند، همچنین جهت سرعت نیز تغییر می‌نماید.
برای تأكید بر اینكه جهت سرعت نیز تغییر می‌كند، شكل سمت راست طوری طراحی شده كه سرعت جسم در نقطه p به نقطه o منتقل گشته است.
زاویه بین دو بردار سرعت با
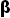نشان داده شده است. از آنجا كه شعاع‌های co و cp بر خطوط مماس (در نقاط o و p) عمودند پس:
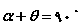
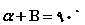
در نتیجه
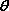و
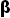با یكدیگر برابرند.
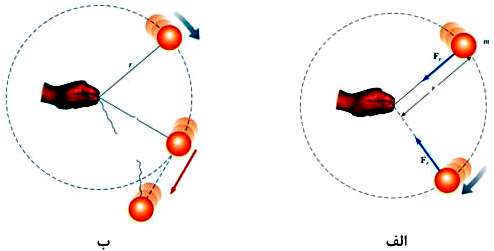
همانند گذشته، شتاب به عنوان نسبت تغییر سرعت به زمان تعریف می‌شود. شكل زیر دو بردار سرعت كه با یكدیگر زاویه
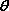می‌سازند را نشان می‌دهد، در ضمن بردار
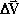نیز در این تصویر رسم شده است.
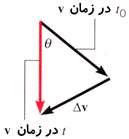
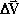برداری است كه اگر به سرعت
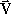در لحظه t[SUB]٠[/SUB] اضافه شود آنگاه سرعت پس از گذشت زمان رابطه زیر را به ما خواهد داد:
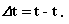
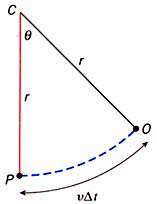
تصویر زیر مقطع pco از دایره را نشان می‌دهد. بدیهی است طول كمان op برابر
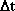V است.
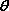كوچك فرض شود (با كوچك در نظر گرفتن
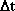) آنگاه زاویه
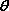را می‌توان به دو صورت بیان نمود (بر حسب رادیان)
(در شكل 1):
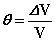
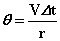
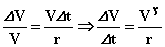
پس شتاب مركزگرا كه بنا به تعریف عبارت از:
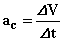
از رابطه‌ای مشابه و ساده تر عبارت زیر قابل محاسبه می‌باشد.
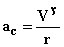
شتاب مركزگرا بردار است پس علاوه بر مقدار دارای جهت نیز می‌باشد. جهت آن همواره به سمت مركز دایره حركت می‌باشد.
مثال زیر این موضوع را به نمایش می‌گذارد.
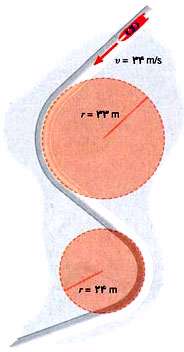
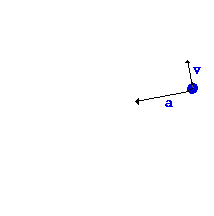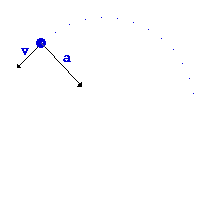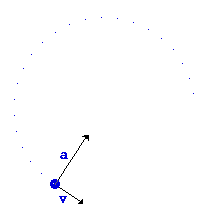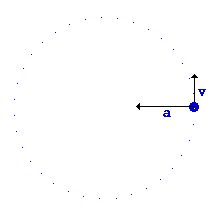
در شكل مقابل جسمی (مثلاً هواپیمای مدل) در مسیر دایروی به صورت یكنواخت حركت می‌كند.
متحرك با (٠) مشخص شده است. این جسم به ناگاه در نقطه o از مسیر دایروی آزاد می‌شود.
(مثلاً نخ كنترل هواپیمای مدل پاره شده است). آیا جسم در مسیر مستقیم oA حركت می‌كند یا مسیر منحنی op؟
[h=2]راهنمایی و حل: قانون اوّل نیوتن مبنای حل مسأله می‌باشد. "جسم در حال سكون باقی می‌ماند یا با تندی ثابت در مسیر مستقیم به حركت خود ادامه می‌دهد مگر آنكه نیروی خالصی بر آن وارد گردد." وقتی جسم رها شود دیگر هیچ نیرویی بر آن وارد نمی‌گردد.
در مثال هواپیمای مدل، با پاره شدن طناب هیچ نیرویی بر آن وارد نمی‌شود (نیروی وزن وارد بر هواپیما با نیروی بالابر بال ها برابر است). با این فرض‌ها بدیهی است كه متحرّك مسیر مستقیم oA را طی خواهد نمود.
تصویر زیر حركت مشابه‌ای را نشان می‌دهد.
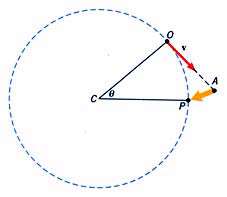
اگر جسم مقید به مسیر می‌بود آنگاه به نقطه p می‌رسید پس مقید بودن به مسیر این امكان را فراهم می‌كند كه متحرك از A به P نقل مكان كند!
همانطور كه مشاهده می‌كند Ap (كمابیش) رو به مركز دایره می‌باشد و اگر زاویه
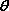كوچك فرض شود آنگاه AP از مركز دایره می‌گذرد.
پس اگر متحرّك بر روی مسیر دایروی حركت كند آنگاه شتاب وارد بر آن رو به مركز دایره خواهد بود در نتیجه به آن شتاب مركزگرا می‌گویند.
اگر عامل تامین كننده شتاب مركزگرا برداشته شود آنگاه متحرك در مسیر مستقیم حركت خواهد نمود.
مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا
در این مبحث خواهید دید كه چگونه اندازه شتاب مركزگرا (a[SUB]c[/SUB]) به اندازه تندی و شعاع حركت ارتباط دارد.
در شكل مقابل یك جسم كه با (٠) نشان داده شده در حال حركت یكنواخت دایروی می‌باشد.
در لحظه t[SUB]٠[/SUB] سرعت آن مماس بر دایره در نقطه o و در لحظه t سرعت آن مماس بر دایره در نقطه p خواهد بود.
در هنگامی كه جسم از o به p حركت می‌كند، شعاع دایره نیز زاویه
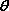
برای تأكید بر اینكه جهت سرعت نیز تغییر می‌كند، شكل سمت راست طوری طراحی شده كه سرعت جسم در نقطه p به نقطه o منتقل گشته است.
زاویه بین دو بردار سرعت با
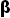
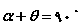
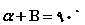
در نتیجه
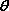
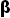
همانند گذشته، شتاب به عنوان نسبت تغییر سرعت به زمان تعریف می‌شود. شكل زیر دو بردار سرعت كه با یكدیگر زاویه
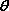
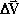
(شكل 1)
بردار
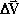
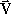
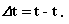
تصویر زیر مقطع pco از دایره را نشان می‌دهد. بدیهی است طول كمان op برابر
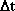
(شکل ٢)
اگر زاویه
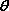
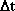
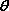
(در شكل 1):
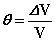
(در شكل ٢):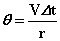
با تركیب این دو رابطه داریم: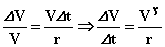
پس شتاب مركزگرا كه بنا به تعریف عبارت از:
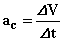
از رابطه‌ای مشابه و ساده تر عبارت زیر قابل محاسبه می‌باشد.
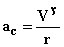
برای مشاهده فیلم کلیک کنید.
شتاب مركزگرا بردار است پس علاوه بر مقدار دارای جهت نیز می‌باشد. جهت آن همواره به سمت مركز دایره حركت می‌باشد.
مثال زیر این موضوع را به نمایش می‌گذارد.
در شكل مقابل جسمی (مثلاً هواپیمای مدل) در مسیر دایروی به صورت یكنواخت حركت می‌كند.
متحرك با (٠) مشخص شده است. این جسم به ناگاه در نقطه o از مسیر دایروی آزاد می‌شود.
(مثلاً نخ كنترل هواپیمای مدل پاره شده است). آیا جسم در مسیر مستقیم oA حركت می‌كند یا مسیر منحنی op؟
[h=2]راهنمایی و حل: قانون اوّل نیوتن مبنای حل مسأله می‌باشد. "جسم در حال سكون باقی می‌ماند یا با تندی ثابت در مسیر مستقیم به حركت خود ادامه می‌دهد مگر آنكه نیروی خالصی بر آن وارد گردد." وقتی جسم رها شود دیگر هیچ نیرویی بر آن وارد نمی‌گردد.
در مثال هواپیمای مدل، با پاره شدن طناب هیچ نیرویی بر آن وارد نمی‌شود (نیروی وزن وارد بر هواپیما با نیروی بالابر بال ها برابر است). با این فرض‌ها بدیهی است كه متحرّك مسیر مستقیم oA را طی خواهد نمود.
تصویر زیر حركت مشابه‌ای را نشان می‌دهد.
اگر جسم مقید به مسیر می‌بود آنگاه به نقطه p می‌رسید پس مقید بودن به مسیر این امكان را فراهم می‌كند كه متحرك از A به P نقل مكان كند!
همانطور كه مشاهده می‌كند Ap (كمابیش) رو به مركز دایره می‌باشد و اگر زاویه
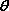
پس اگر متحرّك بر روی مسیر دایروی حركت كند آنگاه شتاب وارد بر آن رو به مركز دایره خواهد بود در نتیجه به آن شتاب مركزگرا می‌گویند.
اگر عامل تامین كننده شتاب مركزگرا برداشته شود آنگاه متحرك در مسیر مستقیم حركت خواهد نمود.
مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا
