فضاي مشبك ، الكتروگراويتي و نيروهاي پيشران و اسپين در فضا

[parisa]

فضاي مشبك ، الكتروگراويتي و نيروهاي پيشران و اسپين در فضا
​

​

​

مقدمه :
قبل از هر چيز از دوست عزيزم جناب آرمين خان متشكرم كه اين پديده فيزيكي را به من معرفي و نكات مهمي را به من يادآوري نمودند .

چكيده :
هنگامي كه خازني با الكترودهاي نامتقارن با ولتاژ بسيار بالا شارژ شود ، يك نيروي پيشران غير عادي به سمت الكترود كوچكتر ظاهر ميشود . اين پديده كه به اثر بيفلد - براون مشهور است اساس كار بسياري از پرنده‌هاي امروزي را تشكيل مي‌دهد . بهترين ركورد منتشر شده براي پرواز اين نوع پرنده‌ها 2.4 متر از [سطح زمين] اعلام شده است . با اين حال هنوز توجيه فيزيكي قابل قبولي براي اين اثر شناخته نشده است .

​

جهت كسب اطلاعات بيشتر فايل PDF زير را به دقت مطالعه فرماييد .
www.ki2100.com/pdf/electro_gravity/electrogravity1.pdf


اينك در اين قسمت سعي مي‌كنيم كه اين پديده شگفت انگيز و همچنين اسپين ذرات باردار در فضا را توجيه كنيم :

همانطور كه ميدانيم اولين نيرو و يا انرژي مهار شده توسط بشر ، انرژي و نيروي باد بود كه بوسيله بادبانها جهت پيش راندن كشتي‌ها استفاده شد . نكته جالب توجه اينكه لازم نبود كه حتما مسير حركت كشتي در امتداد مسير وزش باد قرار مي‌گرفت ، بلكه اين دو مي‌توانستند زاويه‌اي مابين 0 الي 90 درجه داشته باشند . ملوانان با مشاهده تغيير جهت وزش باد ، زاويه بادبانها را تغيير داده و به مسير خود ادامه مي‌دادند و اگر اين زاويه بيشتر از 90 درجه و يا مخالف جهت حركت كشتي مي‌شد ، آنها مجبور بودند بادبانها را پايين كشيده و منتظر تغيير جهت وزش باد بمانند ، حتي اگر اين وضعيت روزها و ماه‌ها به طول مي‌كشيد ، به هر حال چاره‌اي نداشتند جز صبر و انتظار .

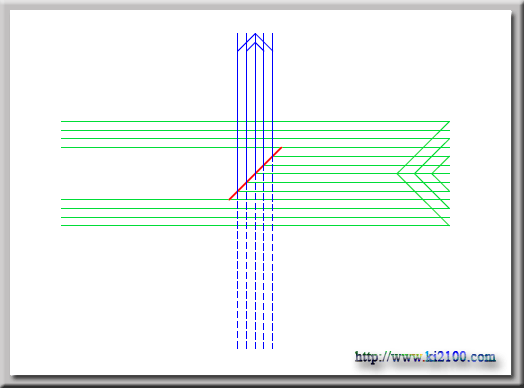
در رسم فوق خطوط و فلش سبز رنگ مسير وزش باد ، پاره خط قرمز رنگ زاويه بادبان و همچنين خطوط و فلش آبي رنگ مسير و جهت حركت كشتي را نشان ميدهد . به اين نيرو ، نيروي پيشران كشتي در آب گفته ميشود . با توجه به اين مسئله ميتوانيم پديده الكتروگراويتي و اسپين ذرات باردار را توجيه كنيم .

​

ما ميتوانيم چنين تصور كنيم كه فضا ساختار مشبكي دارد كه از مكعب‌هاي بسيار كوچكي تشكيل شده است كه هندسه آن كاملا اقليدسي ميباشد ، به اشكال زير توجه نماييد :

همانطور كه مشخص است خطوط به موازات محورهاي x , y , z در فضا امتداد يافته و فضاي مشبكي را تشكيل مي‌دهند . اينك اگر در فضا يك ميدان الكتريكي يكنواخت برقرار شود همانند شكل زير :

​

​

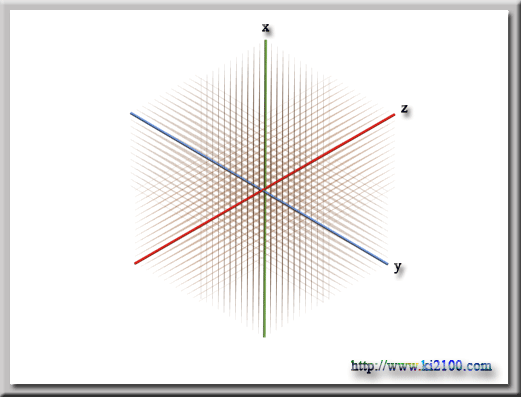
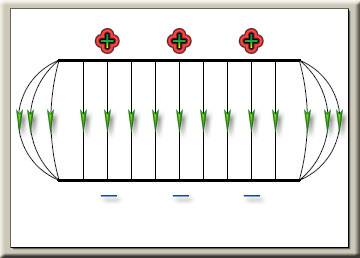
هيچ برهمكنشي مابين اين ميدان الكتريكي و فضاي مشبك بوجود نمي‌آيد . اما اگر در فضا يك ميدان الكتريكي غير يكنواخت با چگالي متفاوت پديدار شود همانند اشكال زير :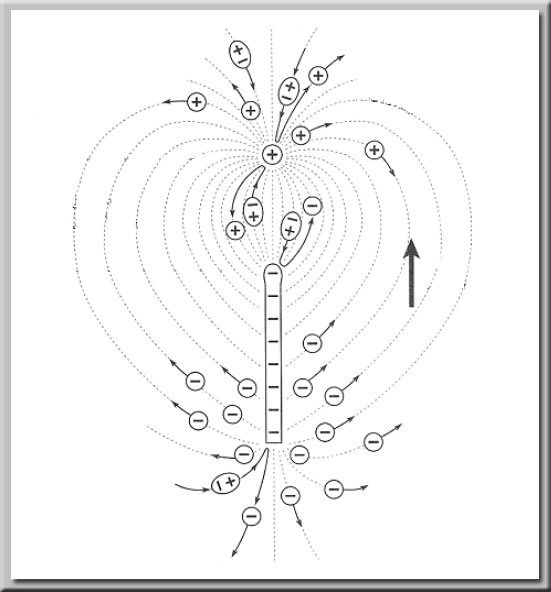

​

​

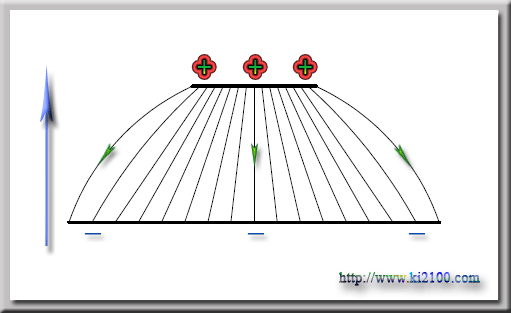
اين ميدان با فضاي مشبك برهمكنش داشته و يك نيروي پيشران به طرف تراكم ميدان الكتريكي با چگالي بالا پديدار ميشود ، يعني شكل زير :

​

خطوط سياه رنگ بيانگر خطوط فضاي مشبك و خطوط آبي رنگ بيانگر خطوط ميدان الكتريكي ميباشد .


اينك وضعيت يك ذره يا گوي باردار در فضاي مشبك را برسي مي‌كنيم :

همانطور كه مشخص است با نزديك شدن به مركز گوي يا ذره باردار به ميزان تراكم ( چگالي ) ميدان الكتريكي افزوده ميشود ،

چون محیط کره کوچکتر میشود به طور مثال دایره فرضی قرمز رنگ نقش الکترود کوچکتر را دارد و همچنین دایره آبی رنگ نقش الکترود بزرگتر را بازی می کند . پس نيروي پيشراني از محيط پيرامون به طرف مركز جرم ( گرانيگاه ، مركز ثقل ) وارد ميشود كه برآيند اين نيروها در كل صفر ميشود و ذره يا گوي در فضا بدون حركت مي‌ماند ، ولي تراكم يا چگالي ميدان الكتريكي در مركز اين ذره يا گوي بشدت افزايش مي‌يابد و ميبايست خنثي شود تا ذره يا گوي به پايداري الكتريكي برسد . براي اين منظور ذره و يا گوي چاره‌اي ندارد جز دوران يا چرخش حول مركز خود تا ميدان الكتريكي آن از حالت خطي به اسپيرال لگاريتمي و يا دايره‌اي و بسته تغيير شكل دهد ، يعني اشكال زير :

مشاهدات ما اين پديده را ثابت مي كند . به طور مثال زماني كه آب درون ظرف شويي به علت نيروي جاذبه براي خروج و دفع پس آب به طرف سيفون حركت مي كند ، با چرخش به صورت گردابي كوچك در مي آيد كه همان شكل مارپيچ فيبوناچي را دارد . ميدان الكتريكي به خود ذره حامل آن نيز نيرو وارد مي كند كه اصطلاحا به اين حالت ( دوران ، چرخش يا سرعت زاويه‌اي ) ذره باردار ، اسپين گفته ميشود . اين سرعت زاويه‌اي ميبايست نيروي پيشران در فضا را نيز خنثي كند .


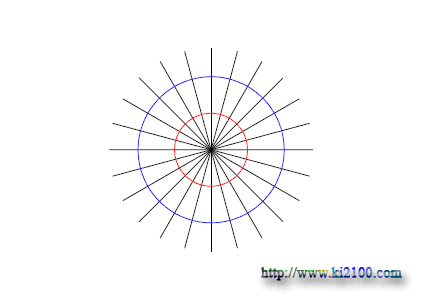
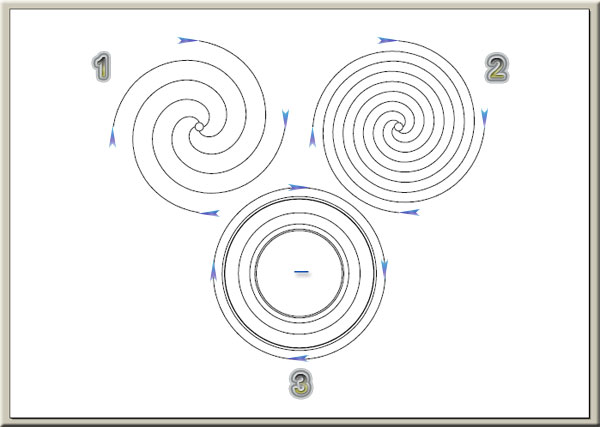
اينك ما اين وضعيت را براي ذره بارداري همچون الكترون برسي مي‌كنيم :


[h=2]ابتدا بايد بدانيم كه انرژي جنبشي دوراني چيست ؟ جسم صلبي را در نظر بگيريد كه با سرعت زاويه‌اي ω حول محوري كه نسبت به يك چهارچوب لخت خاص ثابت است ، می‌چرخد . هر ذره اين جسم در حال دوران ، مقدار معيني انرژي جنبشي دارد . چون تعداد اين ذرات در جسم صلب زياد است ، لذا كميتي به نام لختي دوراني تعريف می‌شود . لختي دوراني به صورت مجموع جملاتي تعريف مي‌شود كه هر جمله با حاصل ضرب جرم يك ذره از جسم صلب در مجذور فاصله عمودي ذره از محور دوران برابر است . بنابراين انرژي جنبشي دوراني جسم صلب كه بخاطر دوران حاصل می‌شود ، برابر است با نصف حاصل ضرب لختي دوراني جسم صلب در مجذور سرعت زاويه‌اي . در حقيقت انرژي جنبشي دوراني الكترون ، حاصل نيروي پيشران وارد بر الكترون است ، يعني همان نيروي الكتروگراويتي وارد بر الكترون .

k=½Iω²​

​

كه k انرژي جنبشي دوراني ، I ممان اينرسي جسم دوار و ω سرعت زاويه‌اي اين دوران است . براي درك اين انرژي يا نيرو فرض مي‌كنيم كه ميدان الكتريكي پيرامون الكترون ، تقارن خود را براي مدتي از دست داده و تمام انرژي جنبشي دوراني آن تبديل به انرژي جنبشي انتقالي شود كه در اين وضعيت الكترون شتاب گرفته و سرعت آن اينچنين بدست مي‌آيد :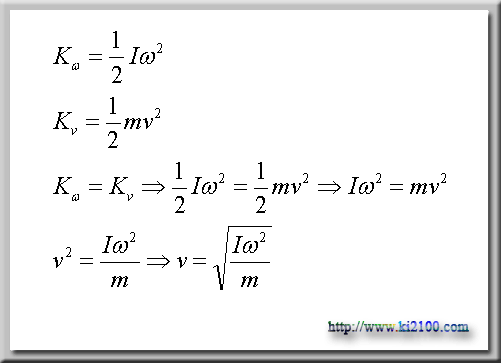

Kω انرژي جنبشي دوراني الكترون ، I لختي دوراني يا ممان اينرسي الكترون ، ω سرعت زاويه‌اي الكترون ، Kv انرژي جنبشي انتقالي الكترون ، m جرم الكترون معادل 9.109534X10[SUP]-31[/SUP] كيلو گرم و v سرعت خطي ( انتقالي ) الكترون ميباشد .
بشقاب پرنده‌ها توان توليد ميدان الكتريكي بسيار قوي ، پيرامون خود را دارند كه با تغيير در چگالي آن ميتوانند به نيروي بسيار زيادي از نوع الكتروگراويتي دست يابند كه اين نيرو ميتواند بي‌وزني و شتاب بسيار زيادي به آنها بدهد .

​

​

اینك میتوانیم توجیهی برای حركت وضعی سیارات و .... ارایه كنیم :
همانطور كه میدانیم شدت میدان گرانشی یا همان g با جرم سیاره رابطه مستقیم ولی با مجذور فاصله رابطه عكس دارد یعنی :

پس میتوان نتیجه گرفت كه میدان گرانشی هم میتواند مثل میدان الكتریكی رفتار كرده و به مركز جرم سیاره نیرو وارد كند و این نیروی وارده با جرم سیاره رابطه مستقیم ولی با مجذور شعاع سیاره رابطه عكس خواهد داشت و ثابت تناسب یك ثابت جدید به نام ثابت حركت وضعی سیاره (S) خواهد بود یعنی :

​

اینك سعی می كنیم كه مقدار این ثابت جدید را اندازه گیری كنیم . جدول زیر رقم بدست آمده برای سیارات منظومه شمسی را نشان می دهد :

​

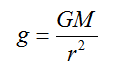
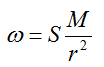
مقدار بدست آمده برای ثابت S​	نام سیاره و یا قمر​

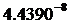
[TD="width: 143, align: center"]

پلوتو​

[/TD]

[TR]
[TD="align: center"]

[/TD]
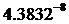
[TD="width: 143, align: center"]زهره[/TD]
[/TR]
[TR]
[TD="align: center"]

[/TD]
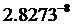
[TD="width: 143, align: center"]

ماه​

[/TD]
[/TR]
[TR]
[TD="align: center"]

[/TD]
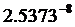
[TD="width: 143, align: center"]عطارد[/TD]
[/TR]
[TR]
[TD="align: center"]

[/TD]
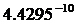
[TD="width: 143, align: center"]مریخ[/TD]
[/TR]
[TR]
[TD="align: center"]

[/TD]
[TD="width: 143, align: center"]زمین[/TD]
[/TR]
[TR]
[TD="align: center"]

[/TD]
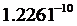
[TD="width: 143, align: center"]اورانوس[/TD]
[/TR]
[TR]
[TD="align: center"]

[/TD]
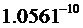
[TD="width: 143, align: center"]نپتون[/TD]
[/TR]
[TR]
[TD="align: center"]

[/TD]
[TD="width: 143, align: center"]زحل[/TD]
[/TR]
[TR]
[TD="align: center"]

[/TD]
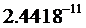
[TD="width: 143, align: center"]مشتری[/TD]
[/TR]

​

همانطور كه مشخص است مقادیر فوق متغیر است و نمی توان از آنها به عنوان یك ثابت در فرمول فوق استفاده كرد ولی آنچكه مسلم است اینكه متوسط چگالي و توزيع آن در سیارات و اقمار منظومه شمسی یكسان نبوده و بعضی از آنها در مجموعه سیارات خاكی و بعضی از آنها مشتری گون هستند و نكته جالب توجه اینكه ، مقادیر بدست آمده در بعضی سیارات و ماه خیلی به هم نزدیك است كه دلیل این پدیده میتواند نزدیكی ساختار فیزیكی سیارت و اقمار به یكدیگر باشد و حدس ما درست بوده و پارامترهای دیگری نیز برای محاسبه حركت وضعی سیارات و اقمار وجود دارد كه اگر در معادله فوق لحاظ شوند ، ثابت S بدست آمده و میتوانیم حركت وضعی اجرام سماوی را بدقت محاسبه كنیم .

محمدرضا طباطبايي