قضیهٔ فیثاغورس در هندسه و فضای اقلیدسی بخشی از صورت کلی قانون کسینوسها هنگامی که زاویهٔ بین دو بردار ۹۰ درجهاست میباشد. این قضیه به نام ریاضیدان یونانی فیثاغورس نامگذاری شدهاست. به سخن دیگر در یک مثلث راستگوشه (قائم الزاویه) همواره مجموع توانهای دوم دو ضلع برابر با توان دوم ضلع سوم است.
قانون کسینوسها بیان میکند که اگر دو بردار (یا خط) a و b در راس O تشکیل یک زاویه با نام A بدهند بردار مجموع از رابطهٔ
 بدست میآید.
بدست میآید.
همانطور که میبینید هر گاه زاویه A برابر با ۹۰ درجه باشد مقدار
 صفر شده و در نتیجه صورت قضیهٔ فیثاغورس بدست میآید:
صفر شده و در نتیجه صورت قضیهٔ فیثاغورس بدست میآید:

وارون این قضیه نیز درست است، به عبارت دیگر، اگر
 باشد، مثلث قائمالزاویه است. اثبات عکس قضیه فیثاغورس را بهاقلیدس نسبت دادهاند.
باشد، مثلث قائمالزاویه است. اثبات عکس قضیه فیثاغورس را بهاقلیدس نسبت دادهاند.
نمایشهای دیگر
اگر c طول وتر مثلث راستگوشه باشد و a و b طول دو ضلع دیگر آن، قضیهٔ فیثاغورس را به شکل رابطهٔ زیر مینویسیم:

و اگر مقدار a و b معلوم باشد c را به این شکل بدست میآوریم:

و اگر c معلوم باشد و یکی از دو ضلع a یا b نامعلوم، آنها را اینگونه بدست میآوریم:

یا

همانگونه که در پیشگفتار بیان شد، قضیهٔ فیثاغورس بخشی از صورت کلی قانون کسینوسها است.
اثبات
قضیهٔ فیثاغورس، قضیهای است که بیش از هر قضیهٔ دیگری اثبات دارد، در کتاب پیشنهاد فیثاغورس (به انگلیسی: The Pythagorean Proposition)، حدود ۳۷۰ اثبات برای این قضیه آورده شدهاست.
اثبات با استفاده از مثلثهای متشابه

این اثبات بر اساس نسبت تناسب میان دو مثلث متشابه بیان شدهاست. به این معنی که اگر دو مثلث متشابه داشته باشیم، نسبتطولهای هر دو ضلع متشابه میان دو مثلث ثابت است.
همان گونه که در شکل نشان داده شدهاست، فرض کنید ABC مثلثی راستگوشهاست و C زاویهای راست (۹۰ درجه) است. حال ارتفاع مثلث را از گوشهٔ C بر وتر AB رسم میکنیم و نقطهٔ برخورد را H مینامیم. نقطهٔ H وتر را به دو بخش d و e تقسیم میکند.
مثلث جدید ACH و مثلث ABC با یکدیگر متشابهاند. چون هر دو یک زاویهٔ ۹۰ درجه دارند (طبق تعریف ارتفاع مثلث) و زاویهٔ A در هر دو مشترک است؛ از این میتوان نتیجه گرفت که زاویهٔ سوم θ در هر دو یکسان است (در شکل نشان داده شدهاست). به دلیل مشابه مثلث CBH نیز با مثلث ABC متشابهاست. به دلیل تشابه مثلثها، روابط زیر برقرار خواهد بود:
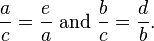
عبارت سمت چپ، برابر است با کسینوس زاویهٔ θ و سمت راست برابر است با سینوس زاویهٔ θ.
این نسبتها را به صورت زیر نیز میتوان نوشت:
 و
و

اگر دو تساوی را با یکدیگر جمع کنیم، خواهیم داشت:
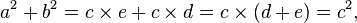
که همان تساوی قضیهٔ فیثاغورس خواهد بود:

روش گفته شده اثبات دانتزیگ، Dantzig بود که یک روش ریاضی بود و بر اساس طولها. این اثبات در تاریخ علم، نقشی قابل توجه داشتهاست. اما سوالی که اینجا مطرح است این است که چرا اقلیدوس از این روش استفاده نکرده و برای اثبات آن روش دیگری را از خود گفتهاست. یک گمان این است که اثبات با استفاده از مثلثهای متشابه نیاز به دانستن تئوری تناسبها داشته که تا آن زمان هنوز مورد بحث قرار نگرفته بود.
اثبات اقلیدوس

خلاصهٔ اثباتی که در کتاب اصول هندسهٔ اقلیدوس نوشته شده چنین است: مربع بزرگ را به دو مستطیل سمت چپ و سمت راست تقسیم میکنیم. یک مثلث ساخته شدهاست که مساحتش نصف مساحت مستطیل سمت چپ است. سپس یک مثلث دیگر ساخته میشود که مساحتش نصف مساحت مربع سمت چپ است. میتوان نشان داد که این دو مثلث با یکدیگر مساویاند درنتیجه مساحت مربع با مساحت مستطیل سمت چپ برابر است. به دلیل مشابه، مطلب گفته شده برای مستطیل سمت راست و مربع دیگر نیز برقرار است. اگر دو مستطیل را کنار هم قرار دهیم تا یک مربع روی وتر مثلث تشکیل دهند، میبینیم که مساحت مربع بزگ (مربعی که روی وتر تشکیل شد) با مجموع مساحتهای دو مربع دیگر برابر است. جزئیات این مطلب در ادامه گفته شدهاست.
فرض کنید A و B و C سه گوشهٔ یک مثلث راستگوشهاند که زاویهٔ A در آن ۹۰ درجهاست. خطی را عمود از گوشهٔ A بر روی وتر BC رسم میکنیم و آن را امتداد میدهیم تا ضلع پایین مربع کشیده شده روی وتر را قطع کند. این خط مربع روی وتر را به دو مستطیل تقسیم میکند که هریک از این مستطیلها مساحتی برابر با مساحت مربعهای رسم شده بر روی دو ضلع زاویهٔ A دارند.
برای ادامهٔ اثبات نیاز به دانستن چند نکتهاست:

شکل جدید مسئله برای بهتر روشن شدن مطلب به همراه خطهای جدید.
ادامهٔ اثبات:
اثبات با استفاده از بازچینی
در نگارهٔ پویای سمت چپ، مساحت کل و مساحت مثلثها همگی ثابت است. بنابراین، مساحت کل ناحیهٔ سیاه رنگ، ثابت است. اما ناحیهٔ اصلی سیاه رنگ با ضلع c را میتوان به دو مربع با ضلعهای a و b تقسیم کرد و نشان داد که: a[SUP]۲[/SUP] + b[SUP]۲[/SUP] = c[SUP]۲[/SUP].
اثبات دوم با استفاده از نگارهٔ پویای میانی است. مربع بزرگ اول، مساحتی برابر با c[SUP]۲[/SUP] دارد با کنار هم قرار دادن چهار مثلث راستگوشهٔ یکسان و به دلیل اختلاف طول ضلع مثلثها، یک مربع کوچک میان آنها و در مرکز مربع بزرگ باقی میماند. اگر یک بار دیگر نگاه کنیم میبینیم که با جابجایی مثلثها، دو مستطیل با ضلعهای a و b تشکیل شدهاست. با ادغام مربع کوچک میانی با یکی از مستطیلها، دو مستطیل به دو مربع تبدیل خواهد شد و مساحت هریک از آنها برابر با a[SUP]۲[/SUP] و b[SUP]۲[/SUP] خواهد بود. بنابراین c[SUP]۲[/SUP] = a[SUP]۲[/SUP] + b[SUP]۲[/SUP]. است.
نگارهٔ سوم سمت راست، نیز خود یک اثبات است. همان گونه که در نگاره نمایش داده شدهاست، دو مربع بالایی، با سایههای آبی و سبز به چندین بخش تقسیم شدهاند. اگر این قسمتهای سایهخورده را کنار هم بچینیم میبینیم که مربع پایینی روی وتر را به خوبی پر میکنند؛ عکس این مطلب نیز برقرار است یعنی مربع پایینی که روی وتر تشکیل شده را میتوان چنان قسمت کرد که دو مربع بالایی به خوبی با این قسمتها پر شود. با این کار نشان دادیم که مساحت مربع بزرگ برابر است با مجموع مساحتهای دو مربع کوچک.[SUP][۹][/SUP]
اثبات جبری

نگارههای مربوط به دو اثبات جبری.
قضیهٔ فیثاغورس را میتوان با استفاده از چیدن چهار مثلث راستگوشهٔ یکسان با ضلعهای a و b و c درون یک مربع با ضلع c به صورت جبری اثبات کرد.مثلثها یکسانند و مساحتی برابر با
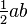 دارند. مربع کوچک ضلعی برابر با b − a و مساحتی برابر با [SUP]۲[/SUP] (b − a) به این ترتیب مساحت مربع بزرگ برابر خواهد بود با:
دارند. مربع کوچک ضلعی برابر با b − a و مساحتی برابر با [SUP]۲[/SUP] (b − a) به این ترتیب مساحت مربع بزرگ برابر خواهد بود با:

و چون این مربع ضلعی برابر با c دارد پس مساحتی برابر با [SUP]۲[/SUP] c خواهد داشت، میتوان نتیجه گرفت:

همان گونه که در پایین نگاره میتوان دید، اثبات مشابه دیگری وجود دارد که در آن با استفاده از بازچینی چهار مربع یکسان به دور مربعی به ضلع c به نتیجه میرسد. با این کار مربع بزرگتری به ضلع (a+b) و در نتیجه با مساحت [SUP]۲[/SUP] (a+b) تشکیل میشود. چهار مثلث و مربع با ضلع c مساحتی برابر با مساحت مربع بزرگتر دارد.
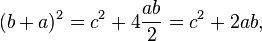
با جابجایی عبارت پشت تساوی خواهیم داشت:

اثبات دیگری برای این قضیه ارائه شدهاست که آن را به جیمز آبرام گارفیلد نسبت میدهند.در این اثبات بجای مربع از یک ذوزنقه استفاده میشود. بخشی از این ذوزنقه از دو نیم کردن (به صورت قطری) مربعی که در اثبات دوم در بالا گفته شد تشکیل شدهاست. مساحت ذوزنقه برابر با نصف مساحت آن مربع است:

نگارهٔ مربوط به اثباتگارفیلد

مربع داخلی نیز دو نیم شدهاست، ادامهٔ اثبات به همان روش مشابهاست با این تفاوت که عامل
 را اضافهتر دارد. که با دو برابر کردن کل عبارت به آسانی حذف میشود.
را اضافهتر دارد. که با دو برابر کردن کل عبارت به آسانی حذف میشود.
اثبات به روش دیفرانسیلی
یک راه اثبات فیثاغورس، نگاه به این مطلب است که با تغییر طول یکی از اضلاع مثلث، در اندازهٔ وتر چه تغییری صورت میگیرد، این کار را باید با استفاده ازحساب دیفرانسیل و انتگرال انجام داد. این نوع اثبات را اثبات به روش اندازهگیری مینامند و از نوع اثبات دانتزیگ است که در آن به اندازهگیری طولها میپردازند و نه مساحتها.
همانگونه که در شکل نشان داده شدهاست، میتوان از دو مثلث راستگوشهٔ ADP و AQP استفاده کرد تا حدهای بالایی و پایینی نسبت دیفرانسیل Δc/Δa را معلوم کرد. بنابراین حد را میتوان از Δa, Δc → 0, گرفت. از نتیجهٔ مشتق dc /da میتوان برای اثبات فیثاغورس استفاده کرد.
از مثلث ABC:

حال مثلث ADP را رسم میکنیم، سپس:


نگارهای که برای بدست آوردن حدهای بالایی و پایینی
 کشیده شدهاست.
کشیده شدهاست.
همان گونه که در قسمت بالای نگاره نشان داده شدهاست، آخرین نامساوی که میتوان از AD> Δc نتیجه گرفت، با ترکیب cos θ در عبارت بدست میآید:
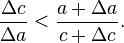
پس از آن مثلث راستگوشهٔ AQP را تشکیل میدهیم (قسمت پایین نگاره) چون هر دو مثلث AQP و PBC یک زاویهٔ
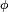 دارند، پس:
دارند، پس:

همانگونه که در نگارهٔ پایینی نمایش داده شدهاست، آخرین نامساوی که میتوان از PQ <Δc نتیجه گرفت، با ترکیب دو نامساوی که از مثلثهای ADP و AQP بدست آمد، ایجاد میشود:
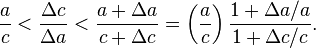
حال حدهای بالایی و پایینی نسبت Δc /Δa را در اختیار داریم. وقتی که Δc و Δa به سمت صفر میل کنند، نسبت Δc /Δa به مشتقdc /da تبدیل میشود و حد بالایی و حد پایینی یکی میشود و خواهیم داشت:

یا

که انتگرالی برابر با مقدار زیر خواهد داشت:
 مقدار ثابت
مقدار ثابت
آنگاه که a = 0 و c = b باشد، مقدار ثابت جواب انتگرال برابر با b[SUP]۲[/SUP] خواهد بود. بنابراین استدلال قضیهٔ فیثاغورس اثبات شد.

وارون قضیه
درستی وارون قضیهٔ فیثاغورس را میتوان اثبات کرد.
فرض کنید ABC مثلثی با اضلاع a و b و c باشد که a[SUP]۲[/SUP] + b[SUP]۲[/SUP] = c[SUP]۲[/SUP]. حال باید ثابت کرد که زاویهٔ میان a و b زاویهای راست است. مثلث دیگری میسازیم با ضلعهای a و b و با یک زاویهٔ راست میان دو ضلع آن، چون میدانیم قضیهٔ فیثاغورس درست است پس طبق این قضیه باید وتر مثلث طولی برابر با c = √(a[SUP]۲[/SUP] + b[SUP]۲[/SUP]) داشته باشد. پس وتر مثلث دوم طولی برابر با وتر مثلث اول دارد. پس دو مثلث با یکدیگر برابرند از هم نهشتی دو مثلث میتوان نتیجه گرفت که زاویههای دو به دو برابر نیز دارند. پس زاویهٔ میان ضلعهای a و b در مثلث اصلی خود، زاویهای راست است.
با استفاده از وارون قضیهٔ فیثاغورس میتوان به آسانی پیدا کرد که یک مثلث زاویهٔ راست، تند یا باز دارد. اگر بزرگترین ضلع یک مثلث را c نامگذاری کنیم، بر اساس نامساوی مثلثهامیتوان گفت a + b> c است (اگر چنین نباشد یعنی مثلثی تشکیل نشدهاست.) حال با استفاده از وارون قضیه فیثاغورس و نامساوی مثلثها میتوان گفت:
sgn(α + β − γ) = sgn(a[SUP]۲[/SUP] + b[SUP]۲[/SUP] − c[SUP]۲[/SUP]),
که در آن α زاویهٔ مقابل به ضلع a و β زاویهٔ مقابل به ضلع b و γ زاویهٔ مقابل به ضلع c است؛ و sgn عبارت تابع علامت میباشد.
کاربردها و نتیجههای قضیه
اعداد فیثاغورسی
اعداد فیثاغورسی به سه عددی میگویند که مجموع مربعهای دو تا از آنها برابر با مربع سومی باشد، به بیان دیگر اعداد a و b و c را فیثاغورسی گویند هرگاه a[SUP]۲[/SUP] + b[SUP]۲[/SUP] = c[SUP]۲[/SUP] باشد. اعداد فیثاغورسی ضلعهای یک مثلث راستگوشه را تشکیل میدهند. بررسیها نشان دادهاست که بناهایی در شمال اروپا وجود داشته که در آنها از ویژگی اعداد فیثاغورسی استفاده میشدهاست و آنها پیش از شناخت این قضیه، از اعداد فیثاغورسی استفاده میکردهاند و آنها را میشناختند. نمونههای پرکاربرد این اعداد عبارتند از: (۳، ۴، ۵) و (۵، ۱۲، ۱۳).
در زیر فهرستی از اعداد فیثاغورسی کوچکتر از ۱۰۰ نوشته شدهاست:
(۳، ۴، ۵)،(۶،۸،۱۰)، (۵، ۱۲، ۱۳)، (۷، ۲۴، ۲۵)، (۸، ۱۵، ۱۷)، (۹، ۴۰، ۴۱)، (۱۱، ۶۰، ۶۱)، (۱۲، ۳۵، ۳۷)، (۱۳، ۸۴، ۸۵)، (۱۶، ۶۳، ۶۵)، (۲۰، ۲۱، ۲۹)، (۲۸، ۴۵، ۵۳)، (۳۳، ۵۶، ۶۵)، (۳۶، ۷۷، ۸۵)، (۳۹، ۸۰، ۸۹)، (۴۸، ۵۵، ۷۳)، (۶۵، ۷۲، ۹۷)، (۱۶۹،۱۲۰،۱۱۹)
نظر ریاضیدانان دربارهٔ قضیه فیثاغورس
کپلر درباره قضیه فیثاغورس نوشتهاست:
قانون کسینوسها بیان میکند که اگر دو بردار (یا خط) a و b در راس O تشکیل یک زاویه با نام A بدهند بردار مجموع از رابطهٔ

همانطور که میبینید هر گاه زاویه A برابر با ۹۰ درجه باشد مقدار


وارون این قضیه نیز درست است، به عبارت دیگر، اگر

نمایشهای دیگر
اگر c طول وتر مثلث راستگوشه باشد و a و b طول دو ضلع دیگر آن، قضیهٔ فیثاغورس را به شکل رابطهٔ زیر مینویسیم:

و اگر مقدار a و b معلوم باشد c را به این شکل بدست میآوریم:

و اگر c معلوم باشد و یکی از دو ضلع a یا b نامعلوم، آنها را اینگونه بدست میآوریم:

یا

همانگونه که در پیشگفتار بیان شد، قضیهٔ فیثاغورس بخشی از صورت کلی قانون کسینوسها است.
اثبات
قضیهٔ فیثاغورس، قضیهای است که بیش از هر قضیهٔ دیگری اثبات دارد، در کتاب پیشنهاد فیثاغورس (به انگلیسی: The Pythagorean Proposition)، حدود ۳۷۰ اثبات برای این قضیه آورده شدهاست.
اثبات با استفاده از مثلثهای متشابه

همان گونه که در شکل نشان داده شدهاست، فرض کنید ABC مثلثی راستگوشهاست و C زاویهای راست (۹۰ درجه) است. حال ارتفاع مثلث را از گوشهٔ C بر وتر AB رسم میکنیم و نقطهٔ برخورد را H مینامیم. نقطهٔ H وتر را به دو بخش d و e تقسیم میکند.
مثلث جدید ACH و مثلث ABC با یکدیگر متشابهاند. چون هر دو یک زاویهٔ ۹۰ درجه دارند (طبق تعریف ارتفاع مثلث) و زاویهٔ A در هر دو مشترک است؛ از این میتوان نتیجه گرفت که زاویهٔ سوم θ در هر دو یکسان است (در شکل نشان داده شدهاست). به دلیل مشابه مثلث CBH نیز با مثلث ABC متشابهاست. به دلیل تشابه مثلثها، روابط زیر برقرار خواهد بود:
عبارت سمت چپ، برابر است با کسینوس زاویهٔ θ و سمت راست برابر است با سینوس زاویهٔ θ.
این نسبتها را به صورت زیر نیز میتوان نوشت:


اگر دو تساوی را با یکدیگر جمع کنیم، خواهیم داشت:
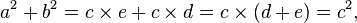
که همان تساوی قضیهٔ فیثاغورس خواهد بود:

روش گفته شده اثبات دانتزیگ، Dantzig بود که یک روش ریاضی بود و بر اساس طولها. این اثبات در تاریخ علم، نقشی قابل توجه داشتهاست. اما سوالی که اینجا مطرح است این است که چرا اقلیدوس از این روش استفاده نکرده و برای اثبات آن روش دیگری را از خود گفتهاست. یک گمان این است که اثبات با استفاده از مثلثهای متشابه نیاز به دانستن تئوری تناسبها داشته که تا آن زمان هنوز مورد بحث قرار نگرفته بود.
اثبات اقلیدوس

فرض کنید A و B و C سه گوشهٔ یک مثلث راستگوشهاند که زاویهٔ A در آن ۹۰ درجهاست. خطی را عمود از گوشهٔ A بر روی وتر BC رسم میکنیم و آن را امتداد میدهیم تا ضلع پایین مربع کشیده شده روی وتر را قطع کند. این خط مربع روی وتر را به دو مستطیل تقسیم میکند که هریک از این مستطیلها مساحتی برابر با مساحت مربعهای رسم شده بر روی دو ضلع زاویهٔ A دارند.
برای ادامهٔ اثبات نیاز به دانستن چند نکتهاست:
- اگر دو ضلع از یک مثلث با دو ضلع از مثلث دیگر یک به یک برابر باشد و زاویهٔ میان آن دو ضلع نیز با هم برابر باشد، میتوان نتیجه گرفت که دو مثلث با یکدیگر برابرند.
- مساحت هر مثلث نصف مساحت چهارضلعی است که اضلاعش با یکدیگر دو به دو موازیاند و ارتفاع و قاعدهای برابر با ارتفاع و قاعدهٔ مثلث دارد.
- مساحت یک مستطیل برابر است با حاصل ضرب دو ضلع مجاورش.
- مساحت یک مربع برابر است با حاصل ضرب دو ضلع از آن.

شکل جدید مسئله برای بهتر روشن شدن مطلب به همراه خطهای جدید.
ادامهٔ اثبات:
- فرض کنید مثلث ABC یک مثلث راستگوشهاست که زاویهٔ CAB در آن ۹۰ درجهاست.
- بر روی هریک از اضلاع BC و AB و CA به ترتیب مربعهای CBDE و BAGF و ACIH رسم شدهاست.
- از گوشهٔ A خطی به موازات BD و CE رسم میکنیم؛ این خط به صورت عمودی با BC و DE بر خورد میکند، محلهای برخورد را به ترتیب K و L مینامیم.
- دو گوشهٔ C را به F و A را به D وصل میکنیم تا مثلثهای BCF و BDA تشکیل شود.
- زاویههای CAB و BAG هر دو زاویههای راستاند. بنابراین نقاط C و A و G بر روی یک امتداد قرار دارند (همخطاند)؛ برای نقاط B و A و H نیز همین مطلب برقرار است.
در این نگاره، دو مثلث مساوی که مساحتی برابر با نصف مساحت مستطیل BDLK و مربع BAGF دارند، نمایش داده شدهاست. - زاویههای CBD و FBA نیز هر دو زاویههای راستاند. درنتیجه دو زاویهٔ ABD و FBC با یکدیگر برابرند چون هردو برابرند با حاصل جمع یک زاویهٔ ۹۰ درجه با زاویهٔ ABC.
- چون AB با FB و BD با BC برابر است؛ درنتیجه مثلث ABD ناگزیر با مثلث FBC برابر خواهد بود.
- چون A-K-L یک خط مستقیم است و با BD نیز موازی است؛ پس BDLK یک چهارضلعی با اضلاع دو به دو موازی است و مساحتی دو برابر مساحت مثلث ABD دارد؛ چون قاعدهٔ BD در هر دو مشترک است و ارتفاع نیز در هر دو طولی برابر با BK دارد.
- چون نقطهٔ C و دو نقطهٔ A و G هر سه بر یک راستا قرار دارند، پس مربع BAGF باید مساحتی دو برابر مساحت مثلث FBC داشته باشد.
- می توان نتیجه گرفت که مساحت مستطیل BDLK، و مربع BAGF با هم برابر است و اندازهٔ آن برابر با AB[SUP]۲[/SUP] است.
- به طور مشابه میتوان نشان داد که مستطیل CKLE مساحتی برابر با مساحت مربع ACIH و برابر با AC[SUP]۲[/SUP] دارد.
- با جمع این دو نتیجه با یکدیگر خواهیم داشت: AB[SUP]۲[/SUP] + AC[SUP]۲[/SUP] = BD × BK + KL × KC
- چون BD = KL و BD* BK + KL × KC = BD(BK + KC) = BD × BC
- چون CBDE یک مربع است پس میتوان نتیجه گرفت که AB[SUP]۲[/SUP] + AC[SUP]۲[/SUP] = BC[SUP]۲[/SUP]
اثبات با استفاده از بازچینی
در نگارهٔ پویای سمت چپ، مساحت کل و مساحت مثلثها همگی ثابت است. بنابراین، مساحت کل ناحیهٔ سیاه رنگ، ثابت است. اما ناحیهٔ اصلی سیاه رنگ با ضلع c را میتوان به دو مربع با ضلعهای a و b تقسیم کرد و نشان داد که: a[SUP]۲[/SUP] + b[SUP]۲[/SUP] = c[SUP]۲[/SUP].
اثبات دوم با استفاده از نگارهٔ پویای میانی است. مربع بزرگ اول، مساحتی برابر با c[SUP]۲[/SUP] دارد با کنار هم قرار دادن چهار مثلث راستگوشهٔ یکسان و به دلیل اختلاف طول ضلع مثلثها، یک مربع کوچک میان آنها و در مرکز مربع بزرگ باقی میماند. اگر یک بار دیگر نگاه کنیم میبینیم که با جابجایی مثلثها، دو مستطیل با ضلعهای a و b تشکیل شدهاست. با ادغام مربع کوچک میانی با یکی از مستطیلها، دو مستطیل به دو مربع تبدیل خواهد شد و مساحت هریک از آنها برابر با a[SUP]۲[/SUP] و b[SUP]۲[/SUP] خواهد بود. بنابراین c[SUP]۲[/SUP] = a[SUP]۲[/SUP] + b[SUP]۲[/SUP]. است.
نگارهٔ سوم سمت راست، نیز خود یک اثبات است. همان گونه که در نگاره نمایش داده شدهاست، دو مربع بالایی، با سایههای آبی و سبز به چندین بخش تقسیم شدهاند. اگر این قسمتهای سایهخورده را کنار هم بچینیم میبینیم که مربع پایینی روی وتر را به خوبی پر میکنند؛ عکس این مطلب نیز برقرار است یعنی مربع پایینی که روی وتر تشکیل شده را میتوان چنان قسمت کرد که دو مربع بالایی به خوبی با این قسمتها پر شود. با این کار نشان دادیم که مساحت مربع بزرگ برابر است با مجموع مساحتهای دو مربع کوچک.[SUP][۹][/SUP]

اثبات با استفاده از بازچینی چهار مثلث راستگوشهٔ یکسان | 
پویانمایی برای نمایش یک اثبات دیگر بوسیلهٔ بازچینی | 
اثبات با استفاده از نمایش ریزهکاریهای بازچینی |
اثبات جبری

نگارههای مربوط به دو اثبات جبری.
قضیهٔ فیثاغورس را میتوان با استفاده از چیدن چهار مثلث راستگوشهٔ یکسان با ضلعهای a و b و c درون یک مربع با ضلع c به صورت جبری اثبات کرد.مثلثها یکسانند و مساحتی برابر با
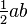

و چون این مربع ضلعی برابر با c دارد پس مساحتی برابر با [SUP]۲[/SUP] c خواهد داشت، میتوان نتیجه گرفت:

همان گونه که در پایین نگاره میتوان دید، اثبات مشابه دیگری وجود دارد که در آن با استفاده از بازچینی چهار مربع یکسان به دور مربعی به ضلع c به نتیجه میرسد. با این کار مربع بزرگتری به ضلع (a+b) و در نتیجه با مساحت [SUP]۲[/SUP] (a+b) تشکیل میشود. چهار مثلث و مربع با ضلع c مساحتی برابر با مساحت مربع بزرگتر دارد.
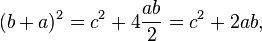
با جابجایی عبارت پشت تساوی خواهیم داشت:

اثبات دیگری برای این قضیه ارائه شدهاست که آن را به جیمز آبرام گارفیلد نسبت میدهند.در این اثبات بجای مربع از یک ذوزنقه استفاده میشود. بخشی از این ذوزنقه از دو نیم کردن (به صورت قطری) مربعی که در اثبات دوم در بالا گفته شد تشکیل شدهاست. مساحت ذوزنقه برابر با نصف مساحت آن مربع است:

نگارهٔ مربوط به اثباتگارفیلد

مربع داخلی نیز دو نیم شدهاست، ادامهٔ اثبات به همان روش مشابهاست با این تفاوت که عامل

اثبات به روش دیفرانسیلی
یک راه اثبات فیثاغورس، نگاه به این مطلب است که با تغییر طول یکی از اضلاع مثلث، در اندازهٔ وتر چه تغییری صورت میگیرد، این کار را باید با استفاده ازحساب دیفرانسیل و انتگرال انجام داد. این نوع اثبات را اثبات به روش اندازهگیری مینامند و از نوع اثبات دانتزیگ است که در آن به اندازهگیری طولها میپردازند و نه مساحتها.
همانگونه که در شکل نشان داده شدهاست، میتوان از دو مثلث راستگوشهٔ ADP و AQP استفاده کرد تا حدهای بالایی و پایینی نسبت دیفرانسیل Δc/Δa را معلوم کرد. بنابراین حد را میتوان از Δa, Δc → 0, گرفت. از نتیجهٔ مشتق dc /da میتوان برای اثبات فیثاغورس استفاده کرد.
از مثلث ABC:

حال مثلث ADP را رسم میکنیم، سپس:


نگارهای که برای بدست آوردن حدهای بالایی و پایینی

همان گونه که در قسمت بالای نگاره نشان داده شدهاست، آخرین نامساوی که میتوان از AD> Δc نتیجه گرفت، با ترکیب cos θ در عبارت بدست میآید:
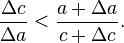
پس از آن مثلث راستگوشهٔ AQP را تشکیل میدهیم (قسمت پایین نگاره) چون هر دو مثلث AQP و PBC یک زاویهٔ

همانگونه که در نگارهٔ پایینی نمایش داده شدهاست، آخرین نامساوی که میتوان از PQ <Δc نتیجه گرفت، با ترکیب دو نامساوی که از مثلثهای ADP و AQP بدست آمد، ایجاد میشود:
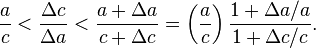
حال حدهای بالایی و پایینی نسبت Δc /Δa را در اختیار داریم. وقتی که Δc و Δa به سمت صفر میل کنند، نسبت Δc /Δa به مشتقdc /da تبدیل میشود و حد بالایی و حد پایینی یکی میشود و خواهیم داشت:

یا

که انتگرالی برابر با مقدار زیر خواهد داشت:

آنگاه که a = 0 و c = b باشد، مقدار ثابت جواب انتگرال برابر با b[SUP]۲[/SUP] خواهد بود. بنابراین استدلال قضیهٔ فیثاغورس اثبات شد.

وارون قضیه
درستی وارون قضیهٔ فیثاغورس را میتوان اثبات کرد.
برای هر سه عدد مثبت a و b و c که در عبارت a[SUP]۲[/SUP] + b[SUP]۲[/SUP] = c[SUP]۲[/SUP] صدق کنند؛ میتوان مثلثی پیدا کرد با طول ضلعهای a و b و c که حتماً دارای زاویهای راست (۹۰ درجه) میان ضلعهای a و b است.
چنین اعدادی را اعداد فیثاغورسی مینامند. بیان دیگر وارون قضیه عبارت است از:
برای هر مثلثی با اضلاع a و b و c اگر a[SUP]۲[/SUP] + b[SUP]۲[/SUP] = c[SUP]۲[/SUP] باشد آنگاه زاویهٔ میان اضلاع a و b برابر با ۹۰ درجه خواهد بود.
بیان استفاده شده در کتاب اصول اقلیدوس (کتاب اول، پیشنهاد ۴۸):
اگر مربع یکی از اضلاع مثلثی برابر باشد با مجموع مربعهای دوضلع دیگر، آنگاه زاویهٔ تشکیل شده با آن دو ضلع، یک زاویهٔ راست است.
درستی این مطلب را میتوان با استفاده از قانون کسینوسها اثبات کرد.
فرض کنید ABC مثلثی با اضلاع a و b و c باشد که a[SUP]۲[/SUP] + b[SUP]۲[/SUP] = c[SUP]۲[/SUP]. حال باید ثابت کرد که زاویهٔ میان a و b زاویهای راست است. مثلث دیگری میسازیم با ضلعهای a و b و با یک زاویهٔ راست میان دو ضلع آن، چون میدانیم قضیهٔ فیثاغورس درست است پس طبق این قضیه باید وتر مثلث طولی برابر با c = √(a[SUP]۲[/SUP] + b[SUP]۲[/SUP]) داشته باشد. پس وتر مثلث دوم طولی برابر با وتر مثلث اول دارد. پس دو مثلث با یکدیگر برابرند از هم نهشتی دو مثلث میتوان نتیجه گرفت که زاویههای دو به دو برابر نیز دارند. پس زاویهٔ میان ضلعهای a و b در مثلث اصلی خود، زاویهای راست است.
با استفاده از وارون قضیهٔ فیثاغورس میتوان به آسانی پیدا کرد که یک مثلث زاویهٔ راست، تند یا باز دارد. اگر بزرگترین ضلع یک مثلث را c نامگذاری کنیم، بر اساس نامساوی مثلثهامیتوان گفت a + b> c است (اگر چنین نباشد یعنی مثلثی تشکیل نشدهاست.) حال با استفاده از وارون قضیه فیثاغورس و نامساوی مثلثها میتوان گفت:
- اگر a[SUP]۲[/SUP] + b[SUP]۲[/SUP] = c[SUP]۲[/SUP], آنگاه مثلث راستگوشهاست.
- اگر a[SUP]۲[/SUP] + b[SUP]۲[/SUP]> c[SUP]۲[/SUP], آنگاه مثلث تیزگوشهاست. (دارای زاویهٔ تند)
- اگر a[SUP]۲[/SUP] + b[SUP]۲[/SUP] <c[SUP]۲[/SUP], آنگاه مثلث دارای زاویهای باز است. (بیش از ۹۰ درجه)
sgn(α + β − γ) = sgn(a[SUP]۲[/SUP] + b[SUP]۲[/SUP] − c[SUP]۲[/SUP]),
که در آن α زاویهٔ مقابل به ضلع a و β زاویهٔ مقابل به ضلع b و γ زاویهٔ مقابل به ضلع c است؛ و sgn عبارت تابع علامت میباشد.
کاربردها و نتیجههای قضیه
اعداد فیثاغورسی
اعداد فیثاغورسی به سه عددی میگویند که مجموع مربعهای دو تا از آنها برابر با مربع سومی باشد، به بیان دیگر اعداد a و b و c را فیثاغورسی گویند هرگاه a[SUP]۲[/SUP] + b[SUP]۲[/SUP] = c[SUP]۲[/SUP] باشد. اعداد فیثاغورسی ضلعهای یک مثلث راستگوشه را تشکیل میدهند. بررسیها نشان دادهاست که بناهایی در شمال اروپا وجود داشته که در آنها از ویژگی اعداد فیثاغورسی استفاده میشدهاست و آنها پیش از شناخت این قضیه، از اعداد فیثاغورسی استفاده میکردهاند و آنها را میشناختند. نمونههای پرکاربرد این اعداد عبارتند از: (۳، ۴، ۵) و (۵، ۱۲، ۱۳).
در زیر فهرستی از اعداد فیثاغورسی کوچکتر از ۱۰۰ نوشته شدهاست:
(۳، ۴، ۵)،(۶،۸،۱۰)، (۵، ۱۲، ۱۳)، (۷، ۲۴، ۲۵)، (۸، ۱۵، ۱۷)، (۹، ۴۰، ۴۱)، (۱۱، ۶۰، ۶۱)، (۱۲، ۳۵، ۳۷)، (۱۳، ۸۴، ۸۵)، (۱۶، ۶۳، ۶۵)، (۲۰، ۲۱، ۲۹)، (۲۸، ۴۵، ۵۳)، (۳۳، ۵۶، ۶۵)، (۳۶، ۷۷، ۸۵)، (۳۹، ۸۰، ۸۹)، (۴۸، ۵۵، ۷۳)، (۶۵، ۷۲، ۹۷)، (۱۶۹،۱۲۰،۱۱۹)
نظر ریاضیدانان دربارهٔ قضیه فیثاغورس
کپلر درباره قضیه فیثاغورس نوشتهاست:
هندسه دو گنج بزرگ دارد: یکی قضیه فیثاغورس است، دیگری تقسیم یک خط به بینهایت نسبت میانگین. ما اولی را با طلا مقایسه میکنیم، دومی را گوهری گرانبها مینامیم.

