محاسبه سرعت نهایی برای محاسبه سرعت نهایی كه گلوله به زمین اصابت میكند به دو سرعت افقی و عمودی در آن لحظه نیاز داریم. در راستای x، سرعت نهایی افقی برابر سرعت اوّلیه افقی خواهد بود زیرا هیچ شتابی در این راستا وجود ندارد.
پس تنها محاسبه مۆلفه y سرعت نهایی باقی میماند. با در اختیار داشتن مۆلفههای سرعت، به راحتی میتوان سرعت نهایی را محاسبه نمود. برای این منظور از قائده فیثاغورث استفاده میكنیم.
به مثال زیر توجّه كنید.

اگر پرتابهای با سرعت افقی ١٩[SUP]m[/SUP]/[SUB]s[/SUB] و سرعت عمودی ٢٣[SUP]m[/SUP]/[SUB]s[/SUB] پرتاب شود. سرعت پرتابه را در لحظه برخورد به تُشك محاسبه نمایید. در ضمن در این پرتاب، محل فرود گلوله ٢m بالاتر از دهانه لوله توپ قرار دارد.
[h=2]

حل: دادههای افقی و عمودی مسأله را با متغیّرهای مناسب مینویسیم و خواهیم داشت:
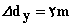
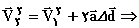

در اینجا دو مقدار برای سرعت به دست آمده است. علامت (+) مربوط به زمانی است كه در ارتفاع ٢m سرعت پرتابه رو به بالا است. این مربوط به لحظات بالا رفتن پرتابه میباشد.
مقدار (-) برای زمانی است كه اگر چه پرتابه در ارتفاع ٢m است ولی این بار در حال پایین آمدن است.

در اینجا ما مقدار V[SUB]2y[/SUB] = -22[SUP]m[/SUP]/[SUB]s[/SUB] را قبول میكنیم زیرا در محل برخورد با زمین، گلوله به سمت پایین در حال حركت است.
با توجّه به مقدار مۆلفه V[SUB]x[/SUB] و V[SUB]y[/SUB] و به كمك قضیه فیثاغورث به راحتی میتوان سرعت نهایی را به دست آورد:

زاویه اصابت گلوله به زمین نیز قابل محاسبه میباشد به طوری كه داریم:

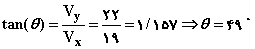
اِمانوئل پاچینی با توپی به طول ١٨m پرتاب شد. وی حدود ٦٤mدر راستای افقی حركت نمود. در تصویر زیر پرتاب وی توسط توپ را مشاهده میكنید:

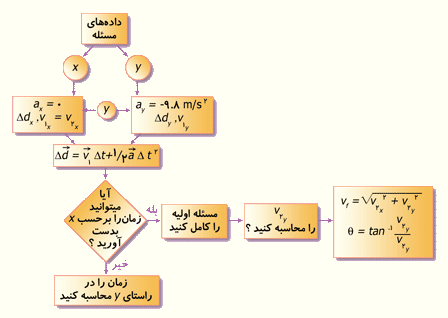
در نمودار زیر نحوه محاسبه سرعت نهایی را مشاهده میكنید.
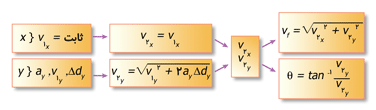
در نمودار زیر مبحث حركت پرتابی خلاصه شده است.
مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا
پس تنها محاسبه مۆلفه y سرعت نهایی باقی میماند. با در اختیار داشتن مۆلفههای سرعت، به راحتی میتوان سرعت نهایی را محاسبه نمود. برای این منظور از قائده فیثاغورث استفاده میكنیم.
به مثال زیر توجّه كنید.

اگر پرتابهای با سرعت افقی ١٩[SUP]m[/SUP]/[SUB]s[/SUB] و سرعت عمودی ٢٣[SUP]m[/SUP]/[SUB]s[/SUB] پرتاب شود. سرعت پرتابه را در لحظه برخورد به تُشك محاسبه نمایید. در ضمن در این پرتاب، محل فرود گلوله ٢m بالاتر از دهانه لوله توپ قرار دارد.
[h=2]

حل: دادههای افقی و عمودی مسأله را با متغیّرهای مناسب مینویسیم و خواهیم داشت:
y = [SUB]ay[/SUB] = -9/8[SUP]m[/SUP]/[SUB]s[SUP]2[/SUP][/SUB]
V[SUB]2y[/SUB] = ?
V[SUB]1y [/SUB]= 23[SUP]m[/SUP]/[SUB]s[/SUB]
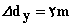
X = V[SUB]x[/SUB] = 19[SUP]m[/SUP]/[SUB]s[/SUB]
a[SUB]x [/SUB]= ?
رابطه مناسب برای مرتبط كردن متغیّرها در راستای (y) عبارتست از: 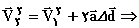

در اینجا دو مقدار برای سرعت به دست آمده است. علامت (+) مربوط به زمانی است كه در ارتفاع ٢m سرعت پرتابه رو به بالا است. این مربوط به لحظات بالا رفتن پرتابه میباشد.
مقدار (-) برای زمانی است كه اگر چه پرتابه در ارتفاع ٢m است ولی این بار در حال پایین آمدن است.

در اینجا ما مقدار V[SUB]2y[/SUB] = -22[SUP]m[/SUP]/[SUB]s[/SUB] را قبول میكنیم زیرا در محل برخورد با زمین، گلوله به سمت پایین در حال حركت است.
با توجّه به مقدار مۆلفه V[SUB]x[/SUB] و V[SUB]y[/SUB] و به كمك قضیه فیثاغورث به راحتی میتوان سرعت نهایی را به دست آورد:

زاویه اصابت گلوله به زمین نیز قابل محاسبه میباشد به طوری كه داریم:

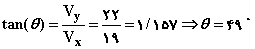
اِمانوئل پاچینی با توپی به طول ١٨m پرتاب شد. وی حدود ٦٤mدر راستای افقی حركت نمود. در تصویر زیر پرتاب وی توسط توپ را مشاهده میكنید:

در نمودار زیر نحوه محاسبه سرعت نهایی را مشاهده میكنید.

در نمودار زیر مبحث حركت پرتابی خلاصه شده است.

مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا
