معادلات هاميلتون

[parisa]

[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]معادلات هاميلتون [FONT=verdana,tahoma,Vazir,helvetica,sans-serif]معادلات هاميلتون از 2n معادله ديفرانسيل درجه اول تشكيل شده است. اين معادلات بر حسب اندازه حركت تعميم يافته و مشتقات آن نوشته مي‌شود. اندازه حركت تعميم يافته به صورت مشتقات تابع لاگرانژي نسبيت به سرعت تعميم يافته تعريف مي‌شود. بنابراين اين معادلات زير خواهند بود.

[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]

​

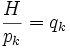
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]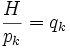

[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]

​

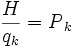
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]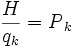
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]در عبارت فوق qk بيانگر سرعت تعميم يافته است و علامت نقطه در بالاي Pk (اندازه حركت تعميم يافته) بيانگر مشتق زماني است. اگر معادلات هاميلتون را با معادلات لاگرانژي مقيسه كنيم ملاحظه مي‌شود كه تعداد اولين معادلات زياد است. يعني اگر سيستم V با N مختصه يافته مشخص شود، در اين صورت معادلات هاميلتون شامل 2n معادله ديفرانسيل درجه اول هستند، در صورتيكه معادلات لاگرانژ از n معادله درجه دوم تشكيل شده است. بنابراين كار كردن با معادلات هاميلتون راحتتر است. معمولا در مكانيك كوانتومي‌ و مكانيك كاري از معادلات هاميلتون استفاده مي‌شود.

 

[parisa]

[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]اصل تغييرات هاميلتون
[FONT=verdana,tahoma,Vazir,helvetica,sans-serif]روش ديگر براي استنتاج معادلات لاگرانژ اصل تغييرات هاميلتوني است. در اين حالت همانگونه كه قبلا نيز اشاره شد در مورد هر سيستم كميتي به نام تابع هاميلتوني تعريف مي‌شود كه برابر با مجموع انرژي جنبشي و انرژي پتانسيل سيستم است. اين اصل در سال 1834 توسط رياضيدان اپرلندي ويليام .ر. هاميلتون ارائه شد.

در اين روش فرض مي‌شود كه يك تابع پتانسيل وجود دارد، يعني سيستم تحت بررسي يك سيستم پاياست. ولي اگر تعدادي از نيروها نيز غير پايستار باشد مانند مورد معادلات لاگرانژ مي‌توان سهم اين نيرو ها را نيز بطور جداگانه منظور كرد. يعني در اين حالت تابع هاميلتون برابر با مجموع انرژي جنبشي و كار انجام شده توسط تمام نيروها اعم از نيروهاي پايستار و غير پايستار است.